La misura dell'anno in astronomia

Il concetto di anno come prospettiva relativa
Sebbene siamo abituati a pensare all'anno terrestre, in realtà ci sono diverse misurazioni possibili
Il concetto di "anno" appare semplice e universale, scandendo le nostre vite con stagioni, festività e compleanni. Eppure, questa misura del tempo, apparentemente così diretta, è una profonda conseguenza di uno dei movimenti del nostro pianeta. Man mano che ci avventuriamo oltre la Terra, la definizione di "anno" si espande in una grande diversità, mettendo in discussione la nostra prospettiva terrestre e rivelando la sorprendente varietà di scale temporali nell'universo.
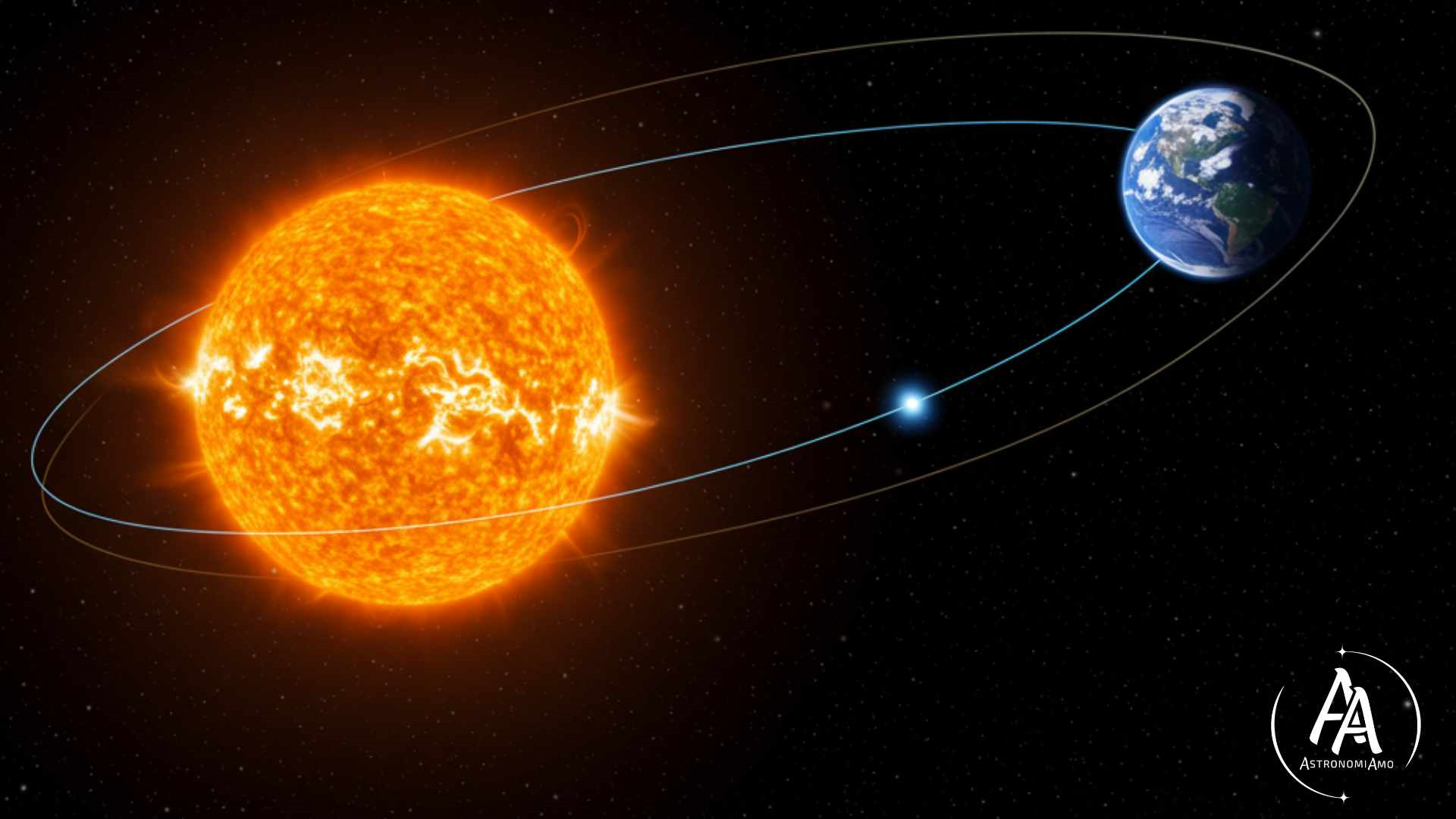
La rivoluzione della Terra attorno al Sole è il moto fondamentale che definisce il nostro anno che, unito all'inclinazione del pianeta rispetto al piano orbitale, definisce le stagioni.
Il concetto di "anno" non è un'unica, semplice definizione nemmeno sulla Terra, ma piuttosto un termine che racchiude diverse misurazioni astronomiche precise, ciascuna legata a un punto di riferimento celeste specifico. Questa precisione è essenziale per l'astronomia.
- Anno Tropico (Anno Solare): Questo è l'anno più rilevante per la nostra vita quotidiana e per i calendari. È il tempo impiegato dal Sole per tornare alla stessa posizione rispetto all'equinozio di primavera. La sua durata media è di 365,24218967 giorni (365 giorni, 5 ore, 48 minuti, 46,98 secondi). Questo anno governa direttamente il ciclo delle stagioni. La sua importanza risiede nel mantenere il nostro calendario sincronizzato con i ritmi naturali dell'agricoltura e delle festività stagionali.
- Anno Siderale: Questo è il vero periodo della rivoluzione terrestre attorno al Sole, misurato rispetto a stelle distanti, considerate "fisse". La sua durata media è leggermente più lunga dell'anno tropico: 365,256363051 giorni (365 giorni, 6 ore, 9 minuti, 10 secondi). La differenza tra l'anno tropico e quello siderale è dovuta alla precessione degli equinozi. Questo fenomeno, un lento ondeggiamento dell'asse terrestre, fa sì che il punto dell'equinozio di primavera si sposti gradualmente verso ovest lungo l'eclittica. Di conseguenza, il Sole raggiunge questo punto leggermente prima di completare un'orbita completa rispetto alle stelle. Questo spostamento, sebbene minimo su base annuale, si accumula nel tempo, rendendo l'anno tropico più corto di circa 20 minuti rispetto all'anno siderale.
- Anno Anomalistico: Questo è il tempo tra due successivi passaggi della Terra attraverso il suo perielio. A causa dell'interferenza gravitazionale di altri pianeti, l'orientamento dell'orbita ellittica terrestre (i suoi apsidi) si sposta lentamente. Questo spostamento, noto come precessione degli apsidi, rende l'anno anomalistico leggermente più lungo dell'anno siderale, con una media di 365,259635864 giorni (365 giorni, 6 ore, 13 minuti, 52 secondi). Questo tipo di anno è particolarmente importante per la previsione di fenomeni come le eclissi, che dipendono dalla posizione della Terra rispetto ai punti estremi della sua orbita.
L'esistenza di queste diverse definizioni di "anno" rivela che il concetto di tempo non è un'entità monolitica, ma una misurazione precisa adattata a specifici fenomeni celesti. L'anno tropico è fondamentale per la vita civile e agricola, l'anno siderale per la navigazione stellare e la mappatura celeste, e l'anno anomalistico per le dinamiche orbitali e le previsioni a lungo termine. Le sottili "oscillazioni" della Terra e i lenti spostamenti orbitali (la precessione degli equinozi e degli apsidi) sono effetti gravitazionali misurabili, causati principalmente dall'influenza della Luna e degli altri pianeti. Questi movimenti, sebbene impercettibili nella vita quotidiana, hanno un impatto cumulativo significativo sulla nostra misurazione fondamentale del tempo e sulle definizioni astronomiche, sottolineando la natura dinamica anche di meccanismi orbitali apparentemente stabili.
Il calendario: una sfida di sincronizzazione con il cosmo
Misurare la durata dell'anno non è stato semplice e non lo è ancora: i calendari vengono modificati proprio per stare dietro alle variazioni della natura
Le civiltà umane hanno a lungo cercato di sincronizzare i propri calendari con i cicli astronomici della Terra, in particolare con l'anno tropico che detta le stagioni. I primi calendari, come quello romano, erano spesso imprecisi e basati su osservazioni lunari, richiedendo aggiustamenti manuali per rimanere allineati con le stagioni.
Il calendario giuliano, introdotto da Giulio Cesare nel 46 a.C. con l'aiuto dell'astronomo Sosigene, rappresentò un significativo passo avanti, stabilendo un anno di 365 giorni con un anno bisestile ogni quattro anni. Questo sistema tentava di compensare le circa 0,25 giorni in più oltre i 365 interi.
Nonostante i suoi miglioramenti, il calendario giuliano era ancora leggermente impreciso, aggiungendo circa 11 minuti di troppo ogni anno. Nel corso di 1600 anni, questo errore si accumulò fino a circa 10 giorni, causando lo slittamento dell'equinozio di primavera astronomico dall'allora convenzionale 21 marzo all'11 marzo. Questo disallineamento creò un problema significativo per la Chiesa, poiché la data della Pasqua, legata all'equinozio di primavera, si stava progressivamente spostando verso l'estate.
Per correggere questo errore, Papa Gregorio XIII promulgò il calendario gregoriano nel 1582. La riforma prevedeva due modifiche principali:
- Eliminazione di dieci giorni: Per riallineare il calendario con l'equinozio astronomico, il giorno successivo al 4 ottobre 1582 divenne il 15 ottobre 1582, cancellando di fatto dieci giorni. Questa misura drastica riportò l'equinozio di primavera al 21 marzo.
- Regole raffinate per gli anni bisestili: Pur mantenendo un anno bisestile ogni quattro anni, gli anni secolari (quelli che terminano con '00', come 1700, 1800, 1900) non sono considerati anni bisestili a meno che non siano divisibili per 400 (ad esempio, il 2000 è stato un anno bisestile, ma il 2100 non lo sarà). Questa regola più precisa riduce la durata media dell'anno a 365,2425 giorni, molto più vicina all'anno tropico reale. Il calendario gregoriano è estremamente accurato, con una discrepanza di soli 26 secondi per anno solare, che si accumulerà in un solo giorno ogni 4909 anni.
I calendari sono invenzioni umane dinamiche, costantemente perfezionate per allinearsi con la realtà astronomica, spesso guidate da esigenze culturali e religiose. La motivazione principale della riforma gregoriana fu l'accurata determinazione della Pasqua, dimostrando come le osservanze religiose possano stimolare il progresso scientifico e le riforme del calendario. Questo evidenzia che la nostra misurazione del tempo è un amalgama di osservazione scientifica e necessità sociali.
È interessante notare che l'adozione storica del calendario gregoriano non fu uniforme e spesso portò a "salti" di giorni in momenti diversi e in luoghi diversi. Mentre alcuni paesi cattolici lo adottarono immediatamente nel 1582 (come l'Italia, la Polonia, il Portogallo e la Spagna), le nazioni protestanti e ortodosse resistettero per secoli, percependo la riforma come un'imposizione papale.
- Francia e alcuni stati cattolici tedeschi e svizzeri: Adottarono il nuovo calendario nel dicembre 1582, saltando anch'essi 10 giorni.
- Paesi Bassi (Province Cattoliche): Adottarono il calendario gregoriano nel dicembre 1582, ma le province protestanti si adeguarono solo nel 1700-1701.
- Gran Bretagna e colonie americane: Adottarono il calendario gregoriano solo nel 1752, quasi due secoli dopo la sua promulgazione. Questo ritardo causò un "salto" di 11 giorni. Nel 1752, il giorno successivo al 2 settembre divenne il 14 settembre. Si crearono persino disordini popolari, con la gente che urlava "Ridateci i nostri 11 giorni!". Questo spiega perché la nascita di George Washington, sebbene ufficialmente celebrata il 22 febbraio 1732, secondo il calendario giuliano sarebbe stata il 11 febbraio 1731 (a causa anche del cambiamento dell'inizio dell'anno civile dal 25 marzo al 1° gennaio).
- Svezia (e Finlandia): Il processo di adozione fu particolarmente confuso e graduale, con un tentativo di passare al calendario gregoriano eliminando gli anni bisestili per 40 anni, dal 1700 al 1740. Questo portò la Svezia a un calendario proprio che non era né giuliano né gregoriano per un certo periodo. Alla fine, nel 1753, la Svezia adottò il calendario gregoriano saltando 11 giorni, ma per rimediare all'errore precedente, il 30 febbraio fu addirittura un giorno valido in Svezia nel 1712!
- Russia: La Russia zarista e poi l'Unione Sovietica mantennero il calendario giuliano fino a dopo la Rivoluzione d'Ottobre (1917). Per questo motivo, la "Rivoluzione d'Ottobre" si verificò in realtà a novembre secondo il calendario gregoriano (il 25 ottobre giuliano corrisponde al 7 novembre gregoriano). La transizione in Russia avvenne nel 1918, con un "salto" di 13 giorni (dal 31 gennaio al 14 febbraio).
- Grecia: La Chiesa Ortodossa Greca adottò un calendario modificato solo nel 1923, che è un calendario giuliano riveduto che concorda con il gregoriano per le date fisse (ma non per la Pasqua, che segue ancora un calcolo ortodosso). Anche qui ci fu un salto di 13 giorni.
Queste discrepanze nell'adozione aggiungono un affascinante strato di storia umana e impatto culturale alla discussione scientifica sulla misurazione del tempo, spiegando perché il Natale ortodosso è ancora oggi celebrato il 7 gennaio (o altre date, a seconda della Chiesa ortodossa che segue ancora il calendario giuliano "vecchio stile").
Il giorno giuliano
Per gli astronomi, le complessità e i cambiamenti storici dei calendari civili rappresentano un problema significativo per la registrazione dei dati a lungo termine. Per superare queste difficoltà, gli astronomi utilizzano le Date Giuliane (JD), un conteggio continuo di giorni e frazioni a partire da un punto di riferimento fisso.
Il sistema del Giorno Giuliano è stato proposto nel 1583 da Joseph Justus Scaliger, che lo chiamò in onore di suo padre, Julius Caesar Scaliger, e non in onore di Giulio Cesare (sebbene la coincidenza con il calendario giuliano sia notevole).
Questo punto di riferimento è stato scelto perché coincide con l'inizio di tre cicli di tempo astronomici: il ciclo indizione (15 anni), il ciclo solare (28 anni) e il ciclo lunare (19 anni). Il prodotto di questi tre cicli ($15 \times 28 \times 19 = 7980$) definisce il "Periodo Giuliano" di 7980 anni.
Il sistema delle Date Giuliane fornisce una cronologia coerente per le osservazioni astronomiche che abbracciano millenni, evitando problemi come gli anni bisestili, i cambi di calendario o le diverse convenzioni nazionali. Per gli astronomi, è fondamentale avere una scala temporale invariante e universale, distinta dai calendari civili culturalmente specifici. Questa distinzione sottolinea le diverse esigenze della ricerca scientifica rispetto alla vita di tutti i giorni.
La Data Giuliana Modificata (MJD) è una variante più semplice, introdotta per comodità, in quanto i numeri JD interi sono diventati molto grandi. La MJD è definita come:
$$ \text{MJD} = \text{JD} - 2400000.5 $$
La MJD inizia a mezzanotte del 17 novembre 1858, che è quando il Giorno Giuliano era $2400000.5$. Questo sposta il punto di riferimento a mezzanotte anziché a mezzogiorno, rendendola più comoda per molte applicazioni moderne.
Siano:
- $Y$: l'anno (es. 2023)
- $M$: il mese (1 per gennaio, 12 per dicembre)
- $D$: il giorno del mese (con frazioni per l'ora del giorno)
Se il mese è gennaio o febbraio, si considera l'anno precedente e si aggiunge 12 al mese. Questo semplifica i calcoli legati ai giorni bisestili.
$$ \text{Se } M \le 2: $$ $$ M = M + 12 $$ $$ Y = Y - 1 $$
Ora, calcoliamo i termini intermedi:
- $A = \text{int}(Y/100)$
- $B = 2 - A + \text{int}(A/4)$
Il valore di $B$ è un termine di correzione per il calendario gregoriano (rappresenta la correzione degli anni bisestili secolari).
Infine, il Giorno Giuliano (JD) si calcola come:
$$ \text{JD} = \text{int}(365.25 \times (Y + 4716)) + \text{int}(30.6001 \times (M + 1)) + D + B - 1524.5 $$
Il termine $-1524.5$ è una costante di offset. Il $.5$ finale si riferisce al fatto che il Giorno Giuliano inizia a mezzogiorno UT.
Esempio: Conversione del 1° gennaio 2000, mezzogiorno UT
Per il 1° gennaio 2000, mezzogiorno UT:
- $Y = 2000$
- $M = 1$
- $D = 1.5$ (per mezzogiorno)
Applichiamo le correzioni per mese:
- $M = 1 + 12 = 13$
- $Y = 2000 - 1 = 1999$
Calcoliamo $A$ e $B$:
- $A = \text{int}(1999/100) = 19$
- $B = 2 - 19 + \text{int}(19/4) = 2 - 19 + 4 = -13$
Ora calcoliamo JD:
$$ \text{JD} = \text{int}(365.25 \times (1999 + 4716)) + \text{int}(30.6001 \times (13 + 1)) + 1.5 + (-13) - 1524.5 $$ $$ \text{JD} = \text{int}(365.25 \times 6715) + \text{int}(30.6001 \times 14) + 1.5 - 13 - 1524.5 $$ $$ \text{JD} = \text{int}(2452338.75) + \text{int}(428.4014) + 1.5 - 13 - 1524.5 $$ $$ \text{JD} = 2452338 + 428 + 1.5 - 13 - 1524.5 $$ $$ \text{JD} = 2438596 $$
Questo valore (2438596) rappresenta il Giorno Giuliano per il mezzogiorno del 1° gennaio 2000, UT.
Gli anni sugli altri pianeti e esopianeti
Trattandosi di una misura locale, è interessante mettere a confronto la durata dell'anno terrestre con quella di altri corpi celesti, solari e non
Gli anni nel Sistema Solare
La durata di un anno varia in modo significativo tra i pianeti del nostro Sistema Solare, discostandosi notevolmente dai 365 giorni terrestri. Questa differenza è principalmente attribuibile a due fattori: la lunghezza del percorso orbitale di ciascun pianeta e l'intensità dell'attrazione gravitazionale del Sole. I pianeti più vicini al Sole hanno orbite più corte e subiscono una maggiore attrazione gravitazionale, il che li costringe a muoversi più velocemente per contrastare tale forza e mantenere la loro orbita. Al contrario, i pianeti più lontani dal Sole percorrono orbite molto più estese e si muovono a velocità inferiori, risultando in anni di durata considerevolmente maggiore.
Questa relazione è elegantemente descritta dalla terza legge di Keplero
Ecco una panoramica dettagliata della durata approssimativa di un anno per ciascun pianeta del Sistema Solare, espressa in giorni e anni terrestri:
| Pianeta | Distanza media dal Sole (milioni di km) | Periodo orbitale (giorni terrestri) | Periodo orbitale (anni terrestri) |
|---|---|---|---|
| Mercurio | 57,91 | 88 | ~0,24 |
| Venere | 108,21 | 225 | ~0,62 |
| Terra | 149,59 | 365 | 1 |
| Marte | 227,94 | 687 | ~1,88 |
| Giove | 778,41 | 4.333 | ~11,86 |
| Saturno | 1.430 | 10.759 | ~29,45 |
| Urano | 2.870 | 30.687 | ~84,01 |
| Nettuno | 4.490 | 60.190 | ~164,88 |
Come si può osservare, l'anno di Mercurio dura meno di un quarto di un anno terrestre, mentre un anno su Nettuno si estende per quasi 165 anni terrestri. Questa enorme disparità evidenzia la vasta gamma di scale temporali che esistono all'interno del nostro stesso sistema stellare.
Peculiarità orbitali e rotazionali: oltre la semplice rivoluzione
Oltre alla semplice durata dell'anno, i pianeti del Sistema Solare presentano una varietà di peculiarità orbitali e rotazionali che li rendono unici. La maggior parte dei pianeti del Sistema Solare segue orbite con basse eccentricità, il che significa che sono quasi circolari. Tuttavia, le comete e gli oggetti della fascia di Kuiper, così come alcuni pianeti extrasolari, possono avere orbite molto più eccentriche.
Un'altra caratteristica distintiva è l'inclinazione assiale. L'asse terrestre è inclinato di circa 23°. Urano, invece, presenta un'inclinazione assiale estrema, quasi di 90 gradi, il che significa che il suo asse di rotazione giace quasi sul piano della sua orbita attorno al Sole. Questa inclinazione insolita porta il pianeta a "rotolare" lungo la propria orbita, esponendo uno dei suoi poli al Sole per metà del periodo di rivoluzione, il che porta a stagioni estremamente lunghe e intense.
Per quanto riguarda la rotazione, la maggior parte dei pianeti del Sistema Solare ruota nello stesso verso in cui orbita attorno al Sole (in senso antiorario se visti dal polo nord celeste). Le uniche eccezioni notevoli sono Venere e Urano. Venere ruota in senso orario (retrogrado), il che significa che un osservatore sulla sua superficie vedrebbe il Sole sorgere a ovest e tramontare a est. Urano, a causa della sua estrema inclinazione assiale, può essere considerato ruotare in senso orario o antiorario a seconda del punto di vista, ma la sua rotazione è essenzialmente "su un fianco".
Alcuni pianeti e pianeti nani, come Nettuno e Plutone, e anche alcuni pianeti extrasolari, mostrano fenomeni di risonanza orbitale. Questo significa che i loro periodi orbitali sono in un rapporto semplice tra loro o con corpi più piccoli, influenzando la stabilità e l'evoluzione delle loro orbite. Ad esempio, Plutone è in risonanza 2:3 con Nettuno, completando due orbite attorno al Sole ogni tre orbite di Nettuno.
Infine, alcuni corpi celesti, in particolare quelli molto vicini alla loro stella, possono essere bloccati marealmente (o in rotazione sincrona), mostrando sempre la stessa faccia alla loro stella. Di conseguenza, su un emisfero è perpetuamente giorno, mentre sull'altro è perpetuamente notte. Questo fenomeno, sebbene non presente nei pianeti maggiori del nostro Sistema Solare, è comune tra i satelliti (come la Luna con la Terra) e tra gli esopianeti più vicini alle loro stelle.
La diversità delle caratteristiche planetarie, dalle inclinazioni assiali estreme alle rotazioni retrograde e alle risonanze orbitali, dimostra che le interazioni gravitazionali e le condizioni di formazione di un sistema stellare possono plasmare orbite e rotazioni in modi sorprendentemente vari. Ogni pianeta è un laboratorio naturale che rivela la ricchezza delle dinamiche celesti.
Oltre il Sistema Solare: gli anni sugli esopianeti
La scoperta di migliaia di esopianeti ha rivelato una diversità di periodi orbitali che supera di gran lunga quella osservata nel nostro Sistema Solare. Questa varietà senza precedenti sfida le nostre precedenti assunzioni sulla formazione e l'evoluzione dei sistemi planetari. Il periodo orbitale, che definisce la durata dell'anno su un esopianeta, è una delle sue caratteristiche primarie e può variare da poche ore a milioni di anni terrestri.
Esempi di anni estremamente brevi: Molti esopianeti scoperti orbitano estremamente vicino alle loro stelle, risultando in anni incredibilmente brevi. Questi includono i cosiddetti "giganti caldi", pianeti massicci simili a Giove che orbitano a distanze molto ravvicinate dalla loro stella.
- PSR J1719-14 b: Questo esopianeta detiene il record per il periodo di rivoluzione più breve in assoluto, completando un'orbita attorno a una pulsar in appena 0,090706293 giorni (circa 2 ore, 10 minuti e 37 secondi). La sua orbita è incredibilmente stretta, a soli 658.230 km dalla sua stella (meno di una volta e mezza la distanza Terra-Luna).
- K2-137 b: Questo pianeta, con un raggio di 0,89 raggi terrestri, orbita attorno a una nana rossa in 0,1797 giorni (circa 4,313 ore). È il pianeta con l'orbita più stretta attorno a una stella di sequenza principale.
- TOI-2109 b: Un gigante caldo scoperto nel 2021, orbita attorno alla sua stella in soli 0,67247 giorni (circa 16,12 ore).
- 55 Cancri e: Noto come "pianeta di lava", ha un periodo orbitale di appena 0,7 giorni.
Esempi di anni estremamente lunghi: All'altro estremo dello spettro, alcuni esopianeti hanno periodi orbitali che si estendono per migliaia o persino milioni di anni terrestri, riflettendo orbite estremamente ampie e distanti dalle loro stelle.
- COCONUTS-2 b: Questo pianeta detiene il record per il periodo orbitale più lungo conosciuto, pari a 1,1 milioni di anni. Orbita a una distanza di 6471 Unità Astronomiche (UA) da una giovane nana rossa.
Questa straordinaria varietà di periodi orbitali è una delle scoperte più affascinanti nel campo degli esopianeti. Il periodo orbitale non è solo una misura del tempo, ma anche un indicatore cruciale della distanza del pianeta dalla sua stella e, di conseguenza, delle condizioni di temperatura superficiale e della potenziale abitabilità.
Ecco alcuni esempi di esopianeti con periodi orbitali notevoli:
| Oggetto | Stella | Periodo (giorni terrestri) | Distanza (a.l.) | Note |
|---|---|---|---|---|
| PSR J1719-14 b | PSR J1719-14 | 0,0907 | - | Periodo più breve in assoluto |
| K2-137 b | K2-137 | 0,1797 | - | Periodo più breve attorno a stella di sequenza principale |
| TOI-2109 b | TOI-2109 | 0,67247 | - | Gioviano caldo con periodo più breve |
| 55 Cancri e | 55 Cancri | 0,7 | - | Super-Terra estremamente calda |
| Proxima b | Proxima Centauri | 11,19 | 4,224 | Esopianeta più vicino alla Terra |
| Kepler-1649 c | Kepler-1649 | 19,5 | 300 | Nella zona abitabile "conservativa" |
| Kepler-442 b | Kepler-442 | 112,3053 | 1291,6 | Nella zona abitabile "conservativa" |
| Kepler-62 f | Kepler-62 | 267 | 981 | Nella zona abitabile "conservativa" |
| Kepler-452 b | Kepler-452 | 385 | 1828 | Nella zona abitabile "ottimistica", simile alla Terra |
| COCONUTS-2 b | COCONUTS-2 | ~401.500.000 | - | Periodo più lungo conosciuto (1,1 milioni di anni) |
Post più popolari

K2-18b: Tra speranza e scetticismo
22/04/2025

Stella polare: cosa è e come trovarla
08/11/2024
Tags
Acqua Astrobiologia Atmosfere planetarie Aurora polare BIblioteche Buchi neri Comete Congiunzioni Corpi celesti Corso Cosmologia Difesa planetaria Eclisse Elettromagnetismo Esopianeti Eventi dal vivo Fenomeni transitori Gravità Infrarosso Inquinamento La Luna Marte Meteorologia spaziale Microonde Missioni Spaziali Moto Occultazioni Opposizioni Osservazione Pianeta Nove Pianeti Quantistica Radiazione Cosmica di Fondo Radiazione Radioastronomia Raggi X Saturno Sistema Solare Sole Stelle e ciclo stellare Storia astronomica Ultravioletto VenereCategorie
Potrebbe interessarti...
Storia della luce: dai corpuscoli alle onde ai quanti
Alla base dell'astronomia, per ...
Leggi di più07/10/2025

Tycho Brahe, il faro dell'astronomia pre-telescopica
Una delle figure più important ...
Leggi di più10/05/2025

 Chi Siamo
Chi Siamo Terra in Vista 2024
Terra in Vista 2024 Relatori
Relatori Argomenti
Argomenti WebTV
WebTV Sole
Sole Luna
Luna Strutture lunari
Strutture lunari Mercurio
Mercurio Venere
Venere Marte
Marte Giove
Giove Satelliti di Giove
Satelliti di Giove Saturno
Saturno Urano
Urano Nettuno
Nettuno Asteroidi
Asteroidi Comete
Comete Bolidi
Bolidi Sciami meteorici
Sciami meteorici ISS
ISS Altri satelliti
Altri satelliti Lanci
Lanci Costellazioni
Costellazioni Stelle
Stelle Profondo cielo
Profondo cielo Esopianeti
Esopianeti Cielo del mese
Cielo del mese Eclissi di Sole
Eclissi di Sole Eclissi di Luna
Eclissi di Luna