Genesi e apogeo del Geocentrismo

Per oltre quattordici secoli, dall'antichità greca fino agli albori dell'età moderna, la visione predominante dell'universo poneva la Terra immobile al centro del cosmo, con il Sole, la Luna, i pianeti e le stelle fisse in orbita attorno ad essa. Questo modello, noto come sistema geocentrico, non fu semplicemente una teoria astronomica, ma una vera e propria visione del mondo che permeò profondamente la cultura, la filosofia e la teologia occidentale e islamica. La sua straordinaria longevità, testimoniata da innumerevoli testi e rappresentazioni artistiche lungo i secoli , non può essere liquidata come semplice frutto di ignoranza o di un dogmatismo imposto dall'autorità religiosa. Al contrario, la sua persistenza derivò da una potente combinazione di fattori: l'apparente evidenza delle osservazioni quotidiane, la sua coerenza interna con la fisica e la filosofia allora dominanti, una notevole (seppur imperfetta) capacità predittiva per gli standard dell'epoca, e la sua profonda integrazione nel tessuto culturale e spirituale del tempo.   

A prima vista, il geocentrismo appariva straordinariamente intuitivo. L'esperienza diretta sembra suggerire inequivocabilmente che la Terra su cui poggiamo i piedi sia solida e stabile, mentre i corpi celesti – il Sole che sorge a est e tramonta a ovest, la Luna con le sue fasi mutevoli, le stelle che compiono una rotazione compatta nel cielo notturno – siano in costante movimento attorno a noi. Questa percezione immediata costituì una base potente e difficile da scardinare per il modello geocentrico. Tuttavia, esso non rimase confinato a una semplice descrizione ingenua. Nel corso dei secoli, evolse da concezioni mitologiche e filosofiche qualitative a sistemi matematicamente sofisticati, culminando nell'opera monumentale di Claudio Tolomeo, l'Almagesto, nel II secolo d.C.. Questo trattato fornì al geocentrismo una base matematica rigorosa, capace di spiegare e prevedere, con un grado di accuratezza notevole per l'epoca, i complessi moti apparenti dei pianeti, incluse le loro enigmatiche retrogradazioni.   

Il successo del modello geocentrico fu ulteriormente rafforzato dalla sua consonanza con la fisica aristotelica, che offriva una spiegazione causale del perché la Terra dovesse trovarsi, immobile, al centro dell'universo, in virtù delle proprietà intrinseche degli elementi che la componevano. Questa coerenza tra astronomia e fisica, unita all'integrazione del modello nella filosofia scolastica e nella teologia cristiana e islamica, creò un paradigma cosmologico straordinariamente robusto e pervasivo.

Lo sviluppo del pensiero geocentrico nel mondo greco antico non fu un percorso lineare, ma piuttosto un complesso intreccio di osservazioni empiriche, speculazione filosofica e innovazione matematica, che gradualmente trasformò le prime intuizioni cosmologiche in modelli sempre più strutturati e quantitativi.

Le prime cosmologie filosofiche greche offrivano già visioni centrate sulla Terra, sebbene con forme diverse. Anassimandro, nel VI secolo a.C., immaginava la Terra come una sezione di colonna o un cilindro, sospeso immobile al centro di tutto, circondato da ruote invisibili perforate attraverso cui si intravedeva un fuoco nascosto (il Sole, la Luna, i pianeti). Nello stesso periodo, Pitagora e i suoi seguaci, pur riconoscendo la sfericità della Terra (probabilmente basandosi sull'osservazione della forma dell'ombra terrestre durante le eclissi lunari), non la collocavano al centro, ma la immaginavano in movimento attorno a un "fuoco centrale" invisibile. Fu la successiva sintesi di queste idee, a partire dal IV secolo a.C., a consolidare il modello che avrebbe dominato per secoli: una Terra sferica, stazionaria, posta al centro dell'universo.   

La convinzione della sfericità terrestre si affermò solidamente nel pensiero greco ben prima di Tolomeo, sfatando il mito moderno di una diffusa credenza antica nella Terra piatta. Già nel V secolo a.C., Empedocle e Anassagora avevano addotto argomenti basati sull'osservazione dell'ombra curva proiettata dalla Terra sulla Luna durante le eclissi lunari. A questa prova si aggiungeva l'esperienza pratica dei marinai, che vedevano apparire all'orizzonte prima la sommità degli alberi delle navi e poi lo scafo, un fenomeno spiegabile solo con la curvatura della superficie marina. Successivamente, astronomi come Aristarco di Samo (III sec. a.C.) ed Eratostene (III-II sec. a.C.) non solo confermarono la sfericità, ma tentarono anche di misurarne le dimensioni con metodi geometrici ingegnosi, basati sull'analisi delle eclissi o sulla misurazione delle ombre proiettate dal Sole in diverse località. Questi sforzi dimostrano l'applicazione precoce della matematica e del ragionamento empirico allo studio del cosmo.   

Nel IV secolo a.C., Platone consolidò filosoficamente l'idea di una Terra sferica e immobile al centro. Nella sua cosmologia, descritta in opere come il Timeo, i corpi celesti (Luna, Sole, cinque pianeti allora conosciuti – Mercurio, Venere, Marte, Giove, Saturno – e le stelle fisse) erano trasportati attorno alla Terra da sfere o cerchi concentrici, in un ordine gerarchico. Platone enfatizzò il principio secondo cui tutti i fenomeni celesti dovessero essere spiegabili attraverso moti circolari uniformi, considerati i più perfetti e adatti alla natura divina dei cieli.   

Fu il suo discepolo, Eudosso di Cnido (circa 380 a.C.), a tradurre questo ideale platonico nel primo modello geometrico-matematico del geocentrismo. Il sistema di Eudosso utilizzava un complesso insieme di sfere omocentriche (concentriche con la Terra) rotanti a velocità diverse e su assi inclinati l'uno rispetto all'altro, per riprodurre i moti apparenti dei pianeti, inclusa la loro retrogradazione, attraverso la combinazione di moti circolari uniformi.   

Aristotele, a sua volta, elaborò e perfezionò il sistema di Eudosso, integrandolo nella sua più ampia visione fisica e metafisica. Aumentò il numero di sfere necessarie per spiegare i moti (fino a 47 o 55) e fornì una base fisica più solida al modello, postulando che le sfere fossero composte di un quinto elemento incorruttibile, l'etere, e che il loro moto fosse legato a un Primo Motore Immobile. La fisica aristotelica, come vedremo, diventerà un pilastro fondamentale a sostegno del geocentrismo.   

Un ulteriore passo verso il modello tolemaico fu compiuto da Ipparco di Nicea (II sec. a.C.), uno dei più grandi astronomi dell'antichità. Sebbene le sue opere originali siano in gran parte perdute, Tolomeo stesso gli attribuisce numerosi contributi fondamentali, tra cui la scoperta della precessione degli equinozi, un accurato catalogo stellare e, soprattutto, l'uso sistematico di modelli geometrici basati su cerchi eccentrici e, probabilmente, sulla combinazione di deferenti ed epicicli (cerchi minori i cui centri si muovono su cerchi maggiori) per spiegare le irregolarità dei moti solare, lunare e planetario.   

Il successo e la persistenza del modello geocentrico non possono essere compresi appieno senza considerare la sua profonda risonanza con l'intuizione immediata e con una visione del mondo fondamentalmente antropocentrica, prevalente sia nell'antichità che nel Medioevo.

Come accennato, l'argomento più potente a favore del geocentrismo derivava dall'esperienza quotidiana. Osservando il cielo da quella che appare come una postazione fissa, si assiste al grandioso spettacolo del Sole che sorge e tramonta, della Luna che attraversa il cielo e delle stelle che ruotano compatte attorno a un punto polare. La Terra, sotto i nostri piedi, appare solida, stabile, immobile. Di fronte a questa evidenza sensoriale diretta, la conclusione che fosse il cielo a muoversi attorno a una Terra stazionaria sembrava non solo ragionevole, ma quasi inevitabile per chi non fosse stato istruito diversamente.  

A questa base intuitiva si sovrapponeva una diffusa visione antropocentrica, la credenza che l'essere umano occupasse una posizione centrale e privilegiata nell'ordine cosmico. Molte culture antiche e medievali ritenevano che l'universo fosse stato creato dagli dei o da Dio specificamente per l'umanità, o che l'uomo ne rappresentasse il fine ultimo. In questo quadro concettuale, appariva "naturale" e coerente che la dimora dell'umanità, la Terra, occupasse anche il centro fisico dell'universo. La centralità geografica diventava così un riflesso e una conferma dell'importanza metafisica e teologica attribuita all'uomo. L'umanità era vista come la "specie prediletta" di Dio, posta al centro di un cosmo creato per suo beneficio.   

Tuttavia, la relazione tra geocentrismo e antropocentrismo è più complessa di quanto suggerisca una lettura superficiale. È stato argomentato che l'idea, diffusa soprattutto dopo la rivoluzione scientifica, secondo cui il geocentrismo fosse esclusivamente una manifestazione di vanità umana ("il mito copernicano") e che l'eliocentrismo l'abbia automaticamente demolita, rappresenti una semplificazione eccessiva della storia. Il geocentrismo aveva, come vedremo, solide basi osservative e fisiche nel contesto del suo tempo, e l'eliocentrismo, a sua volta, non implica necessariamente una visione anti-antropocentrica.   

Inoltre, la visione medievale della centralità terrestre era ambivalente. Se da un lato poteva essere interpretata come un segno di privilegio, dall'altro, all'interno della cosmologia aristotelica adottata dalla Scolastica, la posizione centrale coincideva con il punto più basso dell'universo, il regno della materia pesante, del cambiamento, della corruzione e del peccato (il mondo sublunare), contrapposto alla perfezione, all'immutabilità e alla luce dei cieli superiori (Cieli e sfera sublunare nell'immagine a sinistra, da Philosophia naturalis di Albertus Magnus). In questa prospettiva, essere al centro significava essere nel luogo più infimo e imperfetto, il più lontano dalla purezza divina localizzata nelle sfere più esterne.   

Nonostante queste sfumature, è innegabile che il modello geocentrico abbia fornito per secoli una cornice cosmologica rassicurante, un universo finito, ordinato e gerarchico, in cui l'umanità poteva percepire un "senso di posto" ben definito. La Terra, e con essa l'umanità, era il fulcro attorno al quale ruotava l'intera creazione. Questa visione del mondo, in cui la posizione fisica rispecchiava un ordine morale e spirituale, fu profondamente radicata.   

Si può quindi affermare che la relazione tra geocentrismo e antropocentrismo fosse bidirezionale e storicamente contingente. Una preesistente visione antropocentrica rendeva più plausibile e accettabile un modello cosmico con la Terra al centro. A sua volta, il modello geocentrico, una volta affermatosi anche per le sue ragioni scientifiche e osservative, forniva una potente struttura fisica e visiva che rafforzava, legittimava e dava concretezza alla percezione della centralità umana nel cosmo. Questo ciclo di mutua conferma contribuì a rendere il paradigma geocentrico estremamente resistente al cambiamento. La critica successiva, che tende a etichettare semplicisticamente questa connessione come mera "vanità" umana , rischia di ignorare sia le basi empiriche e fisiche del modello, sia la complessità e l'ambivalenza della concezione medievale della centralità, che poteva implicare tanto il privilegio quanto l'inferiorità. Il passaggio all'eliocentrismo rappresentò, quindi, non solo una rivoluzione scientifica, ma anche una profonda sfida a questa radicata visione antropocentrica e al senso di sicurezza che essa forniva.   

Il modello geocentrico, nella sua forma matura che dominò il pensiero occidentale e islamico per oltre un millennio, poggiava su due pilastri teorici fondamentali:

1. la Fisica qualitativa di Aristotele, che ne forniva la giustificazione causale e la struttura concettuale;
2. la Matematica quantitativa di Tolomeo, che ne permetteva la descrizione precisa e la predizione dei fenomeni celesti.

La Fisica di Aristotele: Il Mondo Sublunare e Celeste

La cosmologia di Aristotele (384-322 a.C.), esposta principalmente nel De Caelo e integrata con i principi della sua Fisica, fornì al geocentrismo una base fisica e metafisica coerente e influente. Il suo sistema si fondava su una dicotomia radicale tra due regioni distinte dell'universo: il mondo sublunare e il mondo celeste o sopralunare.

Il mondo sublunare, che si estendeva dalla superficie terrestre fino all'orbita della Luna inclusa, era il regno dell'imperfezione, del cambiamento, della generazione e della corruzione. Era composto dai quattro elementi classici – terra, acqua, aria e fuoco – che non erano concepiti come sostanze chimiche moderne, ma come portatori di qualità fondamentali quali freddo, caldo, secco e umido. Questi elementi potevano trasformarsi l'uno nell'altro (es. acqua riscaldata diventa vapore, simile all'aria) ed erano soggetti a moti rettilinei, non eterni. La caratteristica fondamentale di questa regione era la sua mutevolezza.   

Al contrario, il mondo celeste, che comprendeva tutto ciò che si trovava al di là della sfera lunare fino ai confini estremi dell'universo, era il regno della perfezione, dell'eternità e dell'immutabilità. Qui non avvenivano né generazione né corruzione. Questa regione era composta da un quinto elemento, l'etere o quintessenza, una sostanza divina, trasparente, priva di peso e incorruttibile, la cui unica proprietà era quella di muoversi eternamente di moto circolare uniforme. I corpi celesti – pianeti, Sole, stelle – erano considerati incastonati in una serie di sfere concentriche fatte di etere (le "sfere cristalline"), che ruotavano attorno alla Terra.   

La chiave per comprendere la struttura geocentrica nella fisica aristotelica risiede nella dottrina del moto naturale. Ogni elemento, secondo Aristotele, possedeva una tendenza intrinseca a muoversi verso il suo "luogo naturale" all'interno del cosmo. Gli elementi pesanti, terra e acqua, tendevano naturalmente a muoversi verso il basso, cioè verso il centro dell'universo. Gli elementi leggeri, aria e fuoco, tendevano invece a muoversi verso l'alto, allontanandosi dal centro e dirigendosi verso la sfera della Luna. Poiché la Terra era composta prevalentemente dall'elemento più pesante, la terra, il suo luogo naturale era il centro stesso dell'universo. Una volta raggiunto il suo luogo naturale, un corpo vi rimaneva in quiete, a meno che non fosse soggetto a un moto violento imposto dall'esterno. Di conseguenza, la Terra doveva essere necessariamente stazionaria al centro del cosmo. Questa spiegazione forniva una potente giustificazione fisica per l'immobilità terrestre, rendendola non un'assunzione arbitraria, ma una conseguenza diretta delle leggi fondamentali della natura come concepite da Aristotele. La stratificazione osservabile (terra solida, oceani d'acqua, atmosfera d'aria, e fenomeni ignei più in alto) era vista come una conferma di questa teoria.   

Il moto dei cieli, invece, era di natura completamente diversa. Il moto naturale dell'etere era circolare e uniforme, considerato il moto più perfetto e adatto alla natura eterna e divina dei corpi celesti. Le sfere celesti ruotavano a velocità diverse e costanti, con la sfera più esterna, quella delle stelle fisse, che possedeva il moto più rapido e primario. L'origine ultima di questo moto eterno era attribuita al Primo Motore Immobile, una causa finale (non efficiente, cioè non "spingeva" le sfere) posta al di là dell'ultima sfera, che muoveva l'universo attirandolo a sé per amore o desiderio, simile a come l'oggetto amato muove l'amante. Questo moto veniva poi trasmesso meccanicamente dalle sfere esterne a quelle interne.   

Sebbene distinti, il mondo sublunare e quello celeste non erano completamente separati. La sfera della Luna, la più interna delle sfere celesti, era considerata a contatto con la regione superiore del mondo sublunare (la sfera del fuoco). Inoltre, i moti celesti, in particolare il percorso annuale del Sole lungo l'eclittica, erano visti come la causa principale dei cambiamenti ciclici nel mondo sublunare, come l'alternarsi delle stagioni e i processi di generazione e corruzione degli esseri viventi.   

In sintesi, la fisica aristotelica non si limitava a descrivere un universo geocentrico, ma forniva una spiegazione causale e qualitativa del perché esso doveva avere quella struttura. La centralità e l'immobilità della Terra, la dicotomia tra mondo terrestre mutevole e cieli eterni, e la perfezione dei moti circolari uniformi erano tutti elementi interconnessi all'interno di un sistema filosofico e fisico completo e coerente. Questa potente sintesi contribuì enormemente a consolidare il paradigma geocentrico e a renderlo il quadro di riferimento indiscusso per secoli.

L'Almagesto di Tolomeo: La matematizzazione dei Cieli

All'interno di questa cornice concettuale di fisica aristotelica fu l'opera dell'astronomo, matematico e geografo Claudio Tolomeo (circa 100-170 d.C.) a dotare il modello di un apparato matematico rigoroso e predittivamente efficace. Il suo trattato monumentale, noto come Almagesto (pagina iniziale nell'immagine a destra), divenne il testo di riferimento per l'astronomia per oltre 1400 anni nel mondo islamico e in Europa. Il titolo originale greco era Mathēmatikḕ Sýntaxis ("Trattato Matematico"), a sottolineare l'approccio quantitativo dell'opera; il nome con cui è universalmente conosciuto deriva dall'arabo al-Majisṭī ("Il Grandissimo"), a testimonianza della sua immensa influenza.   

L'Almagesto, composto da tredici libri, rappresenta la culminazione di secoli di osservazioni e teorie astronomiche ellenistiche e babilonesi. Tolomeo riprese e sistematizzò i lavori dei suoi predecessori, in particolare Ipparco , ma sviluppò un sistema planetario di notevole originalità e complessità matematica. Pur accettando i presupposti fondamentali della cosmologia aristotelica – una Terra sferica, immobile al centro di un universo sferico in rotazione  – l'obiettivo primario di Tolomeo era fornire un modello geometrico capace di "salvare i fenomeni", ovvero di riprodurre e prevedere con la massima accuratezza possibile i moti apparenti dei corpi celesti così come osservati dalla Terra.   

La sfida principale era spiegare le evidenti irregolarità nei moti planetari – le variazioni di velocità, le fluttuazioni di luminosità (e quindi di distanza apparente) e, soprattutto, il fenomeno del moto retrogrado, durante il quale i pianeti sembrano rallentare, fermarsi e invertire temporaneamente la loro direzione di marcia rispetto alle stelle fisse  – mantenendo al contempo, almeno formalmente, il principio del moto circolare uniforme, considerato l'unico adatto ai cieli perfetti.   

Per raggiungere questo scopo, Tolomeo utilizzò e perfezionò un ingegnoso sistema di strumenti geometrici:

Il pianeta (P) si muoveva sulla circonferenza dell'epiciclo. La combinazione del moto del pianeta sull'epiciclo e del moto dell'epiciclo sul deferente permetteva di generare traiettorie complesse (in colore rosso), inclusi i "cappi" che spiegavano il moto retrogrado.   

Questo accorgimento permetteva di spiegare le variazioni nella velocità angolare apparente del pianeta e le sue variazioni di distanza (e quindi luminosità), facendolo apparire più lento all'apogeo (punto più lontano) e più veloce al perigeo (punto più vicino).   

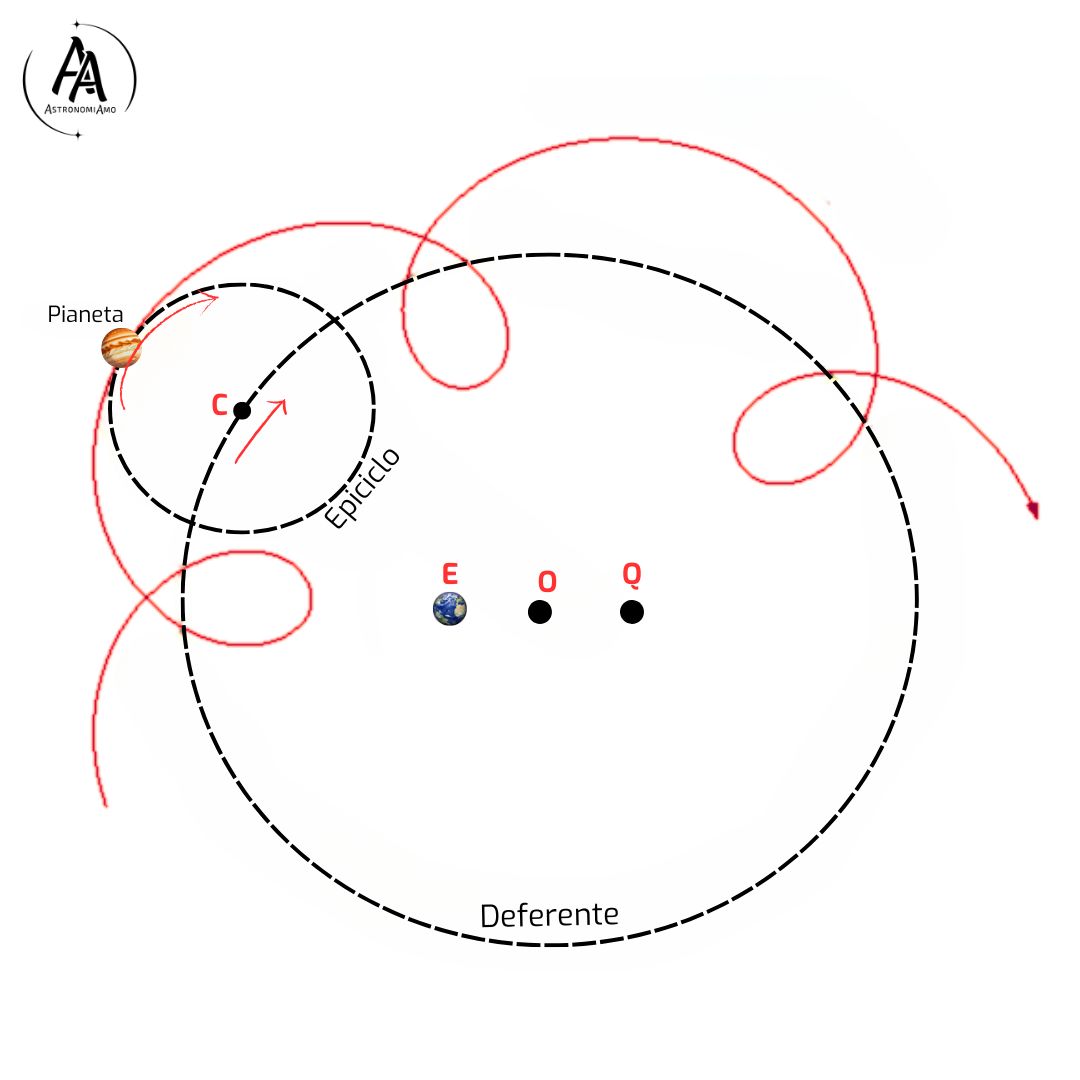Rappresentazione del sistema tolemaico.

L'equante era l'innovazione più significativa e controversa di Tolomeo. Tolomeo postulò che il centro dell'epiciclo (C) si muovesse lungo il deferente in modo tale che la sua velocità angolare fosse costante non rispetto al centro del deferente (O) né rispetto alla Terra (E), ma rispetto al punto equante (Q). Matematicamente, questo significava che l'angolo formato dalla linea QC con una direzione fissa aumentava linearmente nel tempo. Questo complesso meccanismo permetteva di riprodurre con maggiore accuratezza le osservate variazioni di velocità dei pianeti lungo le loro orbite e la diversa durata e forma dei loro moti retrogradi.  

Il sistema tolemaico, quindi, rappresentò un capolavoro di modellizzazione matematica per la sua epoca. Pur radicandosi nei principi fisici del geocentrismo e del moto circolare, Tolomeo dimostrò un approccio pragmatico, quasi strumentalista, dando priorità alla capacità del modello di riprodurre fedelmente le osservazioni ("salvare i fenomeni"). L'introduzione dell'equante ne è l'esempio più lampante: un costrutto matematicamente efficace ma fisicamente problematico, in quanto violava palesemente il principio del moto circolare uniforme attorno al centro geometrico dell'orbita, cardine della fisica aristotelica. Questa tensione intrinseca tra l'esigenza di accuratezza predittiva e la coerenza con i principi fisici fondamentali fu una caratteristica cruciale del sistema tolemaico e divenne uno dei principali bersagli delle critiche successive, in particolare da parte degli astronomi islamici. Tolomeo stesso, in opere successive come le Ipotesi Planetarie, tentò di dare una veste più fisica al suo modello immaginando sfere solide nidificate, ma le contraddizioni tra il modello puramente matematico dell'Almagesto e una sua possibile realizzazione fisica rimasero un punto debole.   

Il modello geocentrico maturo, codificato da Tolomeo, presentava una struttura cosmica ben definita e gerarchica, organizzata in sfere concentriche e dotata di meccanismi specifici per spiegare i moti celesti osservati, sia quelli regolari che quelli apparentemente anomali.

L'ordine delle Sfere Celesti

Al centro immobile dell'universo si trovava la Terra. Attorno ad essa, in una sequenza ordinata e gerarchica, si disponevano le sfere che trasportavano i corpi celesti allora conosciuti. L'ordine standard, procedendo dalla Terra verso l'esterno, era il seguente :   

• Sfera della Luna: Il corpo celeste più vicino alla Terra, segnava il confine tra il mondo sublunare mutevole e il mondo celeste immutabile.   
• Sfera di Mercurio: Il primo dei pianeti.
• Sfera di Venere: Il secondo pianeta.
• Sfera del Sole: Occupava una posizione intermedia cruciale.
• Sfera di Marte: Il primo dei pianeti esterni.
• Sfera di Giove: Il secondo pianeta esterno.
• Sfera di Saturno: Il pianeta più esterno conosciuto nell'antichità.
• Sfera delle Stelle Fisse (Firmamento): La sfera più esterna contenente tutte le stelle, che si riteneva ruotasse come un corpo unico attorno alla Terra, mantenendo fisse le posizioni relative delle stelle (le costellazioni).   

Sebbene Tolomeo nell'Almagesto esprimesse qualche incertezza sull'ordine relativo di Mercurio e Venere rispetto al Sole, la sequenza sopra riportata divenne quella canonicamente accettata nel Medioevo e nel Rinascimento. Questo ordine non era casuale, ma si basava principalmente sui periodi osservati con cui i corpi celesti completavano un giro rispetto alle stelle fisse (periodo siderale): più lento era il moto apparente, più lontana si riteneva fosse la sfera. Mercurio e Venere costituivano un'eccezione parziale a questa regola, poiché i loro periodi medi erano legati a quello del Sole (circa un anno) e la loro posizione nel cielo era sempre vincolata a quella solare (non si trovavano mai in opposizione al Sole). La posizione del Sole, quindi, fungeva da spartiacque naturale tra i pianeti "inferiori" (Mercurio, Venere) e quelli "superiori" (Marte, Giove, Saturno), riflettendo la sua importanza centrale nel determinare i cicli temporali (giorno, anno) e la sua preminenza luminosa.   

Nelle Ipotesi Planetarie, Tolomeo sviluppò ulteriormente questo modello immaginando le sfere come gusci solidi e spessi, nidificati l'uno dentro l'altro senza lasciare spazi vuoti, in modo che l'apogeo di una sfera toccasse il perigeo della sfera successiva. Questo modello "a gusci" permetteva di stimare le distanze relative e assolute dei pianeti dalla Terra, sebbene le stime di Tolomeo (specialmente per il Sole) si rivelassero poi largamente sottostimate.   

Al di là della sfera delle stelle fisse, la concezione variava. Per Aristotele, oltre l'ultima sfera non c'era nulla, nemmeno lo spazio vuoto, ma vi risiedeva concettualmente il Primo Motore Immobile. Nella cosmologia cristiana medievale, come quella di Dante, oltre la sfera delle stelle fisse si trovava il Primo Mobile (la nona sfera, che impartiva il moto diurno a tutte le altre) e, infine, l'Empireo, una decima sfera immateriale, luogo della presenza di Dio, degli angeli e dei beati.   

Questa struttura ordinata e gerarchica forniva una mappa chiara e comprensibile del cosmo, contribuendo alla plausibilità e all'attrattiva del modello geocentrico.

Spiegare i moti celesti: rotazione diurna e percorsi planetari

Il modello geocentrico doveva rendere conto di due tipi principali di movimento osservati nei cieli: il moto diurno comune a tutti i corpi celesti e i moti propri individuali del Sole, della Luna e dei pianeti.

Il moto diurno era il fenomeno più evidente: l'intera volta celeste appariva ruotare come un blocco unico da est a ovest attorno a un asse passante per i poli celesti, completando un giro in circa 24 ore. Questa rotazione spiegava il sorgere e il tramontare quotidiano del Sole, della Luna, dei pianeti e delle stelle. Nel modello geocentrico, questo moto non era attribuito a una rotazione della Terra, ma alla rotazione rapidissima della sfera più esterna (la sfera delle stelle fisse o, in modelli successivi, il Primo Mobile) attorno alla Terra immobile. Si riteneva che questo moto primario venisse poi trasmesso, in qualche modo, a tutte le sfere interne, costringendole a partecipare a questa rotazione giornaliera.   

Oltre a questo moto comune, il Sole, la Luna e i cinque pianeti mostravano un moto proprio, più lento e indipendente, che li portava a spostarsi gradualmente da ovest verso est rispetto allo sfondo delle stelle fisse, lungo o vicino al percorso annuale del Sole (l'eclittica). Ogni corpo celeste completava questo percorso nel suo periodo caratteristico: circa un mese per la Luna, un anno per il Sole, e periodi variabili (da meno di un anno a circa 30 anni) per i pianeti. Questo moto proprio avveniva sulle rispettive sfere o sistemi di deferenti ed epicicli di ciascun corpo celeste.   

Il percorso apparente osservato di un pianeta nel cielo era quindi il risultato complesso della combinazione di questi due moti: il rapido moto diurno est-ovest imposto dalla rotazione della sfera celeste esterna, e il lento moto proprio ovest-est del pianeta all'interno del suo specifico sistema orbitale (deferente/epiciclo).   

Questa netta separazione concettuale tra un moto comune (diurno) imposto a tutto il sistema dall'esterno e un moto proprio (planetario) intrinseco a ciascuna sfera o meccanismo interno fu un elemento chiave del modello geocentrico. Permetteva di trattare analiticamente i due fenomeni in modo distinto: il moto diurno era una rotazione rigida dell'intera struttura, mentre i moti specifici di ciascun pianeta richiedevano la costruzione di modelli geometrici individuali e più complessi per renderne conto.

Giustificare le Anomalie: Moto Retrogrado e Variazioni di Velocità

La vera sfida per il modello geocentrico, e il banco di prova della sua sofisticazione matematica, risiedeva nella spiegazione dei moti planetari che deviavano da un semplice percorso circolare uniforme da ovest a est. Le principali "anomalie" da giustificare erano il moto retrogrado e le variazioni di velocità e luminosità dei pianeti.   

Il moto retrogrado era il fenomeno più vistoso: i pianeti superiori (Marte, Giove, Saturno) e, in modo meno evidente, quelli inferiori (Mercurio, Venere), periodicamente interrompevano il loro moto verso est rispetto alle stelle, rallentavano, si fermavano (stazioni) e si muovevano all'indietro (verso ovest) per un certo periodo, descrivendo spesso un "cappio" o un percorso a "esse" nel cielo, prima di riprendere il loro moto diretto verso est. Inoltre, la velocità apparente dei pianeti lungo l'eclittica non era costante, e la loro luminosità (interpretata come indicatore di distanza) variava ciclicamente, essendo generalmente massima durante il moto retrogrado per i pianeti superiori.   

La soluzione ingegnosa adottata da Tolomeo, basata su idee precedenti di Apollonio e Ipparco, fu quella di utilizzare la combinazione di deferenti ed epicicli. Come descritto, il pianeta non si muoveva direttamente sul deferente, ma su un cerchio più piccolo, l'epiciclo, il cui centro (C) percorreva il deferente attorno alla Terra (E) o a un punto eccentrico (O). Entrambi i moti, quello di C sul deferente e quello del pianeta sull'epiciclo, avvenivano generalmente nella stessa direzione (verso est). Tuttavia, quando il pianeta si trovava nella parte dell'epiciclo più vicina alla Terra (la metà inferiore del cerchio, vista dalla Terra), il suo moto sull'epiciclo avveniva in direzione opposta a quella del moto del centro C sul deferente. Se la velocità del pianeta sull'epiciclo era sufficientemente grande rispetto a quella del centro dell'epiciclo sul deferente, il risultato netto, visto dalla Terra, era un moto apparente verso ovest, cioè retrogrado. Regolando opportunamente i raggi dei due cerchi (R del deferente, r dell'epiciclo) e le loro velocità angolari, era possibile riprodurre i cappi retrogradi osservati.

Tuttavia, il semplice modello deferente-epiciclo non bastava a spiegare tutte le complessità, in particolare le variazioni nella velocità apparente dei pianeti lungo il deferente e le differenze osservate nella durata e nell'ampiezza dei cappi retrogradi. Per questo, Tolomeo introdusse l'eccentrico (spostando il centro del deferente O rispetto alla Terra E) e, soprattutto, l'equante (Q). L'eccentrico contribuiva a spiegare perché un pianeta apparisse muoversi più velocemente quando era più vicino alla Terra (perigeo) e più lentamente quando era più lontano (apogeo). L'equante, imponendo che la velocità angolare del centro dell'epiciclo fosse uniforme rispetto a Q e non a O, permetteva di modulare finemente la velocità del centro dell'epiciclo lungo il deferente, rendendola effettivamente non uniforme rispetto al centro geometrico O e alla Terra E. Questo artificio matematico si rivelò cruciale per migliorare significativamente l'accordo tra le previsioni del modello e le posizioni planetarie osservate.   

Questi strumenti matematici – epicicli, deferenti, eccentrici ed equanti – non devono essere visti come aggiunte arbitrarie o casuali. Essi rappresentavano la risposta tecnicamente più avanzata, all'interno del paradigma geocentrico e della matematica disponibile, ai problemi specifici posti dalle osservazioni astronomiche. La loro introduzione testimonia la notevole flessibilità e la capacità di adattamento del sistema tolemaico nel tentativo di "salvare i fenomeni", anche a costo di introdurre una crescente complessità e di forzare alcuni dei principi filosofici di base, come nel caso dell'equante. Fu proprio questa sofisticata capacità descrittiva a garantire al modello tolemaico il suo lungo dominio.   

La solidità del modello geocentrico non si basava unicamente sulla sua apparente intuitività o sulla sua coerenza con la fisica aristotelica, ma anche su una serie di argomenti ritenuti empiricamente validi all'epoca, volti a dimostrare l'impossibilità fisica del moto terrestre.

La Terra immobile: giustificazioni osservative e fisiche

Diversi argomenti, basati sull'osservazione diretta e su ragionamenti fisici derivati dalla meccanica aristotelica, venivano portati a sostegno della tesi che la Terra fosse immobile al centro dell'universo:

• Mancanza di percezione del moto: L'argomento più immediato era l'assenza di qualsiasi sensazione fisica del movimento terrestre. Se la Terra ruotasse su sé stessa così rapidamente da completare un giro in 24 ore, ci si aspetterebbe di percepire effetti drastici, come un vento perenne e impetuoso che spazzerebbe la superficie in direzione opposta alla rotazione. Poiché tale vento non si manifesta, e gli uccelli possono volare tranquillamente in ogni direzione, si concludeva che la Terra dovesse essere ferma;
• Caduta dei gravi: Un argomento fisico considerato molto forte era quello della caduta dei gravi. Si osservava che un oggetto pesante, come una pietra, lasciato cadere da una certa altezza (ad esempio, dalla cima di una torre), cadeva verticalmente verso il basso, atterrando direttamente ai piedi del punto di lancio. Si ragionava che se la Terra fosse stata in rotazione verso est, durante il tempo di caduta dell'oggetto, il suolo si sarebbe spostato verso est sotto di esso. Di conseguenza, l'oggetto sarebbe dovuto atterrare a ovest del punto di lancio. Poiché l'esperienza mostrava una caduta perfettamente verticale, ciò veniva interpretato come una prova inconfutabile dell'immobilità terrestre. Questo argomento ignorava il principio di inerzia, che sarebbe stato compreso solo secoli dopo;   
• Moto Naturale Aristotelico: Come già discusso, la fisica aristotelica forniva una spiegazione intrinseca all'immobilità terrestre. Essendo composta dagli elementi pesanti (terra e acqua), la cui natura è quella di tendere verso il centro dell'universo e di rimanervi in quiete una volta raggiunto, la Terra si trovava nel suo luogo naturale e non aveva alcuna tendenza intrinseca a muoversi. Qualsiasi moto della Terra sarebbe stato un moto "violento", contrario alla sua natura, e avrebbe richiesto una forza esterna costante per essere mantenuto, cosa che non si osservava;
• Centralità dalle osservazioni celesti: Tolomeo stesso, nell'Almagesto, argomentava a favore della centralità (e implicitamente dell'immobilità) della Terra basandosi sull'osservazione che, in qualsiasi momento e da qualsiasi luogo, esattamente metà della sfera celeste (con le stelle) è visibile sopra l'orizzonte, mentre l'altra metà è nascosta sotto di esso. Se la Terra fosse stata significativamente spostata dal centro dell'universo, questa divisione perfettamente simmetrica del cielo visibile e invisibile non sarebbe stata possibile.   
• Luminosità costante di Venere: Un altro argomento osservativo, sebbene più sottile e basato su un'interpretazione errata, riguardava la luminosità apparente del pianeta Venere. Si notò che la sua brillantezza nel cielo non variava in modo così drastico come ci si sarebbe aspettato se la sua distanza dalla Terra fosse cambiata notevolmente, come previsto dal modello eliocentrico. Questa apparente costanza di luminosità fu interpretata come un'indicazione che Venere si mantenesse a una distanza relativamente stabile dalla Terra, il che sembrava più compatibile con un'orbita geocentrica (probabilmente epiciclica) che con un'orbita eliocentrica. Oggi sappiamo che la maggiore vicinanza di Venere alla Terra nelle sue fasi "nuove" o "crescenti" (quando è tra noi e il Sole) è compensata dalla minore porzione illuminata visibile, risultando in una luminosità complessiva che varia meno di quanto ci si potrebbe aspettare intuitivamente.   

È fondamentale riconoscere che questi argomenti, pur rivelatisi errati alla luce della fisica moderna, erano considerati scientificamente validi e persuasivi nel contesto delle conoscenze e delle teorie fisiche accettate all'epoca. Non si trattava di mere affermazioni basate sulla fede o sul senso comune acritico, ma di deduzioni logiche basate su osservazioni (o mancate osservazioni, come nel caso del vento o della deviazione nella caduta dei gravi) interpretate attraverso il filtro della fisica aristotelica. La confutazione efficace di questi argomenti richiese non solo nuove osservazioni (rese peraltro possibili dal telescopio), ma soprattutto lo sviluppo di una nuova fisica – quella di Galileo, Keplero e Newton – che introducesse concetti rivoluzionari come l'inerzia, la relatività del moto e la gravitazione universale.   

Il Problema della Parallasse Stellare

Accanto agli argomenti basati sulla fisica terrestre, un'altra obiezione potente e di natura prettamente astronomica al moto della Terra, in particolare al suo moto di rivoluzione annuale attorno al Sole (come proposto da Aristarco e poi da Copernico), era l'assenza di parallasse stellare osservabile.   

Applicando il concetto di parallasse al contesto astronomico, se la Terra orbitasse attorno al Sole la nostra posizione nello spazio cambierebbe enormemente nell'arco di sei mesi (spostandoci da un lato all'altro dell'orbita). Questo spostamento dovrebbe causare un cambiamento apparente nella posizione delle stelle più vicine rispetto a quelle più distanti, un effetto noto come parallasse stellare annua. Le stelle vicine dovrebbero apparire spostarsi leggermente avanti e indietro nel corso dell'anno rispetto allo sfondo delle stelle remote, e le configurazioni geometriche delle costellazioni dovrebbero subire lievi deformazioni periodiche.   

Tuttavia, nonostante gli sforzi e la consapevolezza del problema, gli astronomi antichi e medievali non furono in grado di rilevare alcun effetto di parallasse stellare. Le posizioni relative delle stelle apparivano immutabili nel corso dell'anno, compatibilmente con l'idea che fossero fissate su un'unica sfera rigida in rotazione.   

Di fronte a questa mancata osservazione, si presentavano due possibili conclusioni logiche:

1. La Terra è immobile: Se la Terra non si sposta nello spazio, non c'è cambiamento nel punto di osservazione e quindi non ci si aspetta alcuna parallasse. Questa era la conclusione più semplice e diretta, e fu quella adottata dalla stragrande maggioranza degli astronomi greci e medievali, rafforzando il modello geocentrico.   
2. Le stelle sono estremamente lontane: L'alternativa era postulare che le stelle fossero così incredibilmente distanti dalla Terra e dal Sole che lo spostamento angolare dovuto alla parallasse fosse troppo piccolo per essere misurato con gli strumenti dell'epoca. Questa fu l'ipotesi avanzata da Aristarco di Samo nel III secolo a.C. per difendere il suo modello eliocentrico  e fu ripresa da Copernico nel XVI secolo. Tuttavia, questa ipotesi richiedeva di accettare un universo di dimensioni vastissime, ordini di grandezza maggiore di quanto comunemente concepito (dove la sfera delle stelle era immaginata non molto al di là di Saturno ), il che appariva a molti inverosimile o non necessario.   

L'assenza di parallasse stellare osservabile rappresentò quindi uno degli argomenti scientifici più solidi e persistenti contro l'eliocentrismo per quasi duemila anni. Fu solo nel 1838 che Friedrich Bessel riuscì finalmente a misurare la parallasse di una stella (61 Cygni), grazie all'uso di telescopi potenti e tecniche di misurazione precise, fornendo così la prova osservativa diretta del moto di rivoluzione della Terra che era mancata per così tanto tempo.   

Questo episodio storico illustra in modo emblematico come l'interpretazione dell'evidenza scientifica (o della sua assenza) sia profondamente influenzata dal quadro teorico e dalle assunzioni cosmologiche preesistenti. L'assenza di parallasse non "provava" in senso assoluto il geocentrismo, ma lo supportava fortemente all'interno del paradigma dominante di un universo relativamente compatto. Per accettare l'eliocentrismo nonostante la mancanza di parallasse osservabile, era necessario compiere un audace salto concettuale, non solo adottando un nuovo modello per il sistema solare, ma anche rivoluzionando la percezione della scala stessa dell'universo e della distanza delle stelle. Era una richiesta di credere in distanze interstellari immense, basata sulla coerenza teorica del modello eliocentrico piuttosto che su prove dirette, il che spiega in parte le resistenze incontrate da questa idea per lungo tempo.   

Nonostante il suo indiscusso successo e la sua lunga egemonia, il sistema tolemaico non fu esente da problemi e critiche, che emersero progressivamente nel corso dei secoli, ben prima dell'avvento di Copernico. Queste sfide provenivano sia da difficoltà interne al modello stesso, sia da critiche esterne mosse da astronomi e filosofi, in particolare nel fiorente mondo intellettuale islamico medievale.

Crescenti discrepanze e complessità del Modello

Con il passare del tempo e il pur lento miglioramento delle tecniche osservative, emersero alcune debolezze intrinseche al modello tolemaico:

• Problemi di accuratezza predittiva: sebbene l'Almagesto fornisse tavole astronomiche che permettevano di calcolare le posizioni future dei pianeti con un'accuratezza senza precedenti per l'epoca, queste previsioni non erano perfette. Nel lungo periodo, si accumulavano discrepanze tra le posizioni calcolate e quelle effettivamente osservate, rendendo necessarie periodiche revisioni e aggiustamenti dei parametri del modello.   
• Complessità percepita: il sistema tolemaico, con la sua combinazione di deferenti, epicicli, eccentrici ed equanti per ciascun pianeta (ad eccezione del Sole e della Luna, che avevano modelli leggermente più semplici), appariva indubbiamente complesso. Sebbene il mito popolare delle "decine di epicicli su epicicli" per spiegare ogni minima deviazione sia probabilmente un'esagerazione retorica successiva, creata per enfatizzare la presunta semplicità del modello copernicano, la necessità di utilizzare un apparato geometrico così articolato e, in parte, controintuitivo, alimentava un senso di artificiosità e mancanza di eleganza.   
• Violazione dei principi fisici: il punto più vulnerabile del sistema dal punto di vista filosofico e della coerenza interna era l'equante. Come già sottolineato, questo punto fittizio permetteva di mantenere una velocità angolare costante per il centro dell'epiciclo, ma non rispetto al centro del deferente, violando così il principio aristotelico fondamentale del moto circolare uniforme attorno al centro naturale del moto. Questa "mostruosità matematica", come fu definita da alcuni critici, rappresentava una concessione pragmatica all'accuratezza osservativa a scapito della purezza dei principi fisici su cui il modello stesso pretendeva di fondarsi.   
• Problemi specifici e incoerenze: il modello presentava difficoltà particolari nel descrivere accuratamente il moto di alcuni corpi celesti. Il modello lunare di Tolomeo, ad esempio, pur riproducendo correttamente le longitudini, implicava una variazione della distanza Terra-Luna (e quindi del diametro apparente della Luna) molto maggiore di quella effettivamente osservata. Anche il moto di Mercurio, con la sua orbita particolarmente eccentrica e inclinata, si rivelò ostico da modellare con precisione. Inoltre, emergevano tensioni tra la descrizione puramente matematica dei meccanismi nell'Almagesto e il tentativo di darne un'interpretazione fisica in termini di sfere solide e contigue nelle Ipotesi Planetarie. Come potevano sfere materiali interpenetrarsi o muoversi secondo le regole complesse degli epicicli e degli equanti? E in più: il passaggio delle comete, che tagliavano il cielo, come poteva essere coerente con sfere fisiche che ne sarebbero state distrutte?   

Questa crescente complessità e le tensioni interne non erano solo questioni di gusto estetico o filosofico. Riflettevano la difficoltà intrinseca del paradigma geocentrico nel rendere conto in modo semplice e coerente di un insieme di dati osservativi sempre più ricco e preciso. Ogni aggiustamento introdotto per "salvare" un fenomeno specifico rischiava di compromettere la coerenza fisica o filosofica del sistema complessivo, creando un circolo vizioso di complessificazione e incoerenza latente.

Critiche Storiche e Aggiustamenti

Le debolezze del sistema tolemaico non passarono inosservate. Già nell'antichità, figure come Aristarco avevano proposto alternative radicali, sebbene senza successo immediato. Tuttavia, fu soprattutto nel mondo islamico, tra l'VIII e il XVI secolo, che l'astronomia tolemaica fu sottoposta a un'analisi critica sistematica e approfondita, portando a significative correzioni e sviluppi. Gli astronomi islamici non si limitarono a tradurre e preservare l'Almagesto ma lo studiarono criticamente, confrontandolo con nuove osservazioni e principi filosofici.   

• Correzione di parametri e dati: fin dai primi tempi, gli astronomi islamici verificarono e corressero diversi parametri numerici forniti da Tolomeo. Ad esempio, osservazioni indipendenti condotte già nel IX secolo portarono a un valore più accurato per la costante di precessione degli equinozi rispetto a quello riportato da Tolomeo. Astronomi come al-Battani (IX-X sec.) dimostrarono che l'apogeo solare non era fisso rispetto alle stelle, come credeva Tolomeo, ma si muoveva lentamente. Ibn Yunus (X-XI sec.) individuò errori nei calcoli di Tolomeo sulla precessione. Questi lavori evidenziarono la necessità di un continuo aggiornamento osservativo e la fallibilità anche delle autorità più consolidate.   
• Critica all'equante e alle Incoerenze fisiche: la critica più profonda e persistente mossa dagli astronomi islamici riguardò proprio l'equante e la discrepanza tra i modelli matematici tolemaici e una possibile realtà fisica. Figure come Ibn al-Haytham (Alhazen, XI sec.), nel suo influente trattato Al-Shukūk ʿalā Baṭlamyūs ("Dubbi su Tolomeo"), misero in discussione la legittimità di utilizzare costrutti matematici come l'equante, che violavano i principi fisici fondamentali (moto uniforme attorno al centro) e non potevano corrispondere al moto reale di sfere fisiche. Egli sostenne che un modello astronomico dovesse essere non solo matematicamente predittivo, ma anche fisicamente coerente. Questa critica metodologica aprì la strada alla ricerca di modelli alternativi.   
• Sviluppo di modelli geocentrici alternativi: stimolati da queste critiche, diversi astronomi islamici tentarono di costruire nuovi modelli planetari che eliminassero le caratteristiche più problematiche del sistema tolemaico (in particolare l'equante), pur rimanendo all'interno del quadro geocentrico. 
  • La Scuola di Maragha, un importante centro di ricerca astronomica fondato nel XIII secolo nell'attuale Iran, fu particolarmente prolifica in questo senso. Astronomi come Nasir al-Din al-Tusi (XIII sec.), Mu'ayyad al-Din al-Urdi (XIII sec.) e Ibn al-Shatir (XIV sec., operante a Damasco) svilupparono ingegnosi dispositivi geometrici per riprodurre i moti planetari osservati usando esclusivamente combinazioni di moti circolari uniformi. Lo strumento più famoso fu la "coppia di Tusi", un meccanismo composto da due cerchi, uno che rotola all'interno dell'altro (con raggio doppio), capace di generare un moto lineare rettilineo per un punto sulla circonferenza del cerchio interno a partire da moti circolari uniformi. Utilizzando la coppia di Tusi e altri meccanismi simili, questi astronomi riuscirono a costruire modelli per la Luna e i pianeti che eliminavano l'equante tolemaico e rispettavano il principio del moto circolare uniforme, raggiungendo un'accuratezza predittiva paragonabile, se non superiore, a quella di Tolomeo. È particolarmente significativo che i modelli sviluppati da Ibn al-Shatir per il moto della Luna e di Mercurio siano matematicamente identici a quelli che sarebbero stati utilizzati da Niccolò Copernico due secoli dopo.   
  • Anche nell'Andalusia islamica (Spagna) vi fu un'intensa attività critica nei confronti di Tolomeo, sebbene tradizionalmente caratterizzata come più filosofica e legata all'aderenza stretta ai principi della fisica aristotelica. Pensatori come Ibn Rushd (Averroè, XII sec.), Ibn Tufayl (XII sec.) e al-Bitruji (XII sec.) criticarono l'uso di eccentrici ed epicicli in quanto non conformi a un universo di sfere perfettamente concentriche rotanti attorno al centro del mondo (la Terra). Al-Bitruji tentò persino di proporre un modello alternativo basato unicamente su sfere omocentriche, sulla scia di Eudosso e Aristotele, ma i suoi risultati furono poco accurati dal punto di vista predittivo. Ricerche più recenti, tuttavia, hanno messo in discussione la netta separazione tra una critica "filosofica" occidentale e una "matematica" orientale, evidenziando come anche gli astronomi andalusi si occupassero di problemi matematici e osservativi, e viceversa.   
• Discussioni sulla rotazione terrestre: è interessante notare come alcuni eruditi islamici, come il grande scienziato al-Biruni (X-XI sec.) e l'astronomo Abu Sa'id al-Sijzi (X-XI sec.), discussero apertamente la possibilità che fosse la Terra a ruotare sul proprio asse a spiegare il moto diurno dei cieli, anziché l'intera sfera celeste. Sebbene questa idea non si sia tradotta in un modello eliocentrico completo e non sia stata ampiamente accettata, dimostra una notevole apertura mentale e la capacità di mettere in discussione anche i pilastri fondamentali del geocentrismo.   

Queste critiche e riforme, sviluppatesi lungo molti secoli nel mondo islamico, non portarono all'abbandono del geocentrismo, ma rappresentarono un sofisticato programma di ricerca volto a "correggere" e "razionalizzare" l'astronomia tolemaica dall'interno, cercando di risolvere le sue contraddizioni e di renderla più coerente con i principi fisici e filosofici accettati. La portata e la profondità di questo lavoro critico sono state pienamente riconosciute solo dalla storiografia recente. Sebbene manchi ancora una prova documentale definitiva del percorso di trasmissione diretta di queste idee all'Europa rinascimentale, le impressionanti somiglianze matematiche tra i modelli della scuola di Maragha e quelli di Copernico suggeriscono fortemente una continuità intellettuale. L'astronomia islamica medievale, quindi, non fu una semplice custode passiva del sapere greco, ma un laboratorio vivace di critica e innovazione che creò strumenti concettuali e matematici essenziali, preparando, forse inconsapevolmente, il terreno per la successiva rivoluzione eliocentrica.   

L'Osservazione di Alfonso X di Castiglia

Un aneddoto, sebbene di dubbia autenticità storica ma molto citato, illustra bene il crescente disagio nei confronti della complessità del sistema tolemaico anche al di fuori degli ambienti strettamente accademici. Si narra che Alfonso X (1221-1284), re di Castiglia e León, noto come "El Sabio" (Il Saggio o Il Dotto) per il suo vasto patrocinio culturale e scientifico , dopo aver ascoltato una dettagliata spiegazione del complesso meccanismo di epicicli ed equanti necessari per descrivere i moti planetari secondo Tolomeo, abbia commentato: "Se il Signore Onnipotente mi avesse consultato prima di intraprendere la creazione, gli avrei raccomandato qualcosa di più semplice".   

Alfonso X fu un importante mecenate delle scienze e delle arti. Promosse la traduzione di numerose opere dall'arabo al castigliano e commissionò la compilazione delle famose Tavole Alfonsine, un insieme di tavole astronomiche per calcolare le posizioni dei corpi celesti, basate sul sistema tolemaico ma aggiornate con osservazioni più recenti, molte delle quali condotte da astronomi ebrei e musulmani alla sua corte di Toledo. Queste tavole divennero lo standard di riferimento in Europa per diversi secoli.   

Il re operava quindi pienamente all'interno del paradigma geocentrico e della visione del mondo cristiana del suo tempo. Tuttavia, la citazione a lui attribuita, vera o apocrifa che sia, cattura un sentimento di insoddisfazione estetica e filosofica di fronte all'intricata macchinosità del modello tolemaico. Essa suggerisce che un universo creato da un Dio onnipotente e saggio avrebbe dovuto possedere una struttura più armoniosa e meno farraginosa.   

La persistenza di questo aneddoto nel corso dei secoli è significativa. Indica che la percezione di una complessità eccessiva e quasi "innaturale" del sistema tolemaico non era limitata ai soli specialisti impegnati nelle critiche tecniche, ma era diventata un tema riconoscibile, un punto debole avvertito anche a livello culturale più ampio. Questo disagio verso la complessità, pur non portando Alfonso X o i suoi contemporanei a rifiutare il modello dominante, anticipa uno dei criteri – quello della semplicità e dell'armonia matematica – che saranno invocati, seppur in modo non sempre lineare, dai sostenitori del nascente modello eliocentrico come segno della sua maggiore "verità" o "correttezza" rispetto all'ormai vetusto edificio tolemaico.   

Rappresentazioni Visive: Arte e Miniature

Le arti visive, in particolare le miniature che adornavano i manoscritti medievali, offrono una testimonianza vivida di come veniva concepito e raffigurato il cosmo geocentrico. Questi manoscritti, spesso prodotti in contesti monastici e poi in botteghe urbane, illustravano testi di varia natura – scientifici, filosofici, teologici, letterari – e le loro immagini servivano non solo a decorare, ma anche a spiegare, a rendere visibile e memorabile la struttura dell'universo.   

La rappresentazione più comune era quella basata su diagrammi a cerchi concentrici. Al centro si trovava la Terra, spesso raffigurata con elementi geografici stilizzati (montagne, mari). Attorno ad essa si disponevano le sfere celesti in ordine gerarchico: la Luna, i cinque pianeti (Mercurio, Venere, Sole – considerato un pianeta in questo contesto – Marte, Giove, Saturno), e infine la sfera delle stelle fisse, talvolta rappresentata con i segni dello zodiaco. Spesso, sotto la sfera della Luna, venivano raffigurate anche le sfere dei quattro elementi (terra, acqua, aria, fuoco) a sottolineare la distinzione tra mondo sublunare e celeste. In alcune rappresentazioni più elaborate, si aggiungevano sfere superiori come il Primo Mobile o sfere angeliche, talvolta sostenute da angeli. Sebbene la maggior parte di questi diagrammi fosse semplificata, alcuni tentavano di incorporare elementi più complessi del sistema tolemaico, come percorsi planetari non perfettamente circolari o sovrapposti, suggerendo la presenza di epicicli.   

Un'altra modalità di rappresentazione era quella simbolica o antropomorfica, basata su associazioni derivate dall'astrologia e dalla mitologia classica. I pianeti potevano essere raffigurati come figure umane o divinità con attributi specifici: il Sole come un re o un auriga su un carro fiammeggiante, la Luna come una fanciulla o Diana cacciatrice, Mercurio come un messaggero alato o uno studioso, Venere come una dea dell'amore, Marte come un guerriero, Giove come un sovrano saggio, Saturno come un vecchio malinconico. Queste personificazioni, anch'esse di origine classica, si ritrovano in manoscritti prodotti in diverse aree geografiche, testimoniando una tradizione iconografica condivisa. Legata a questa visione era anche l'immagine dell'Uomo Zodiacale, in cui le diverse parti del corpo umano erano messe in corrispondenza con i segni dello zodiaco, riflettendo l'idea del microcosmo umano come specchio del macrocosmo universale.   

Anche dopo l'introduzione del modello eliocentrico da parte di Copernico nel 1543, le rappresentazioni visive del sistema geocentrico continuarono ad essere prodotte e a circolare ampiamente per tutto il XVI e XVII secolo, spesso in opere a stampa come trattati di cosmografia, atlanti e mappe celesti. Esemplificative sono le incisioni del Cosmographical Glasse di William Cunningham (1559), che mostra Atlante sorreggere un universo geocentrico, le illustrazioni per il De sphaera di Sacrobosco , o le magnifiche tavole dell'Harmonia Macrocosmica di Andreas Cellarius (pubblicato a partire dal 1660), che dedica diverse mappe alla dettagliata illustrazione del sistema tolemaico. Spesso, in queste opere tardive, il modello tolemaico veniva presentato accanto ai sistemi concorrenti di Tycho Brahe e di Copernico, a volte come modello ormai superato, altre volte come una delle possibili ipotesi cosmologiche. Anche grandi artisti del Rinascimento, come Raffaello nella celebre "Scuola di Atene" (1509-1511) negli appartamenti vaticani, inclusero la figura di Tolomeo, raffigurato con in mano un globo terrestre, come rappresentante dell'astronomia classica.   

Queste rappresentazioni visive, dai semplici diagrammi dei manoscritti medievali alle elaborate incisioni rinascimentali, svolsero un ruolo cruciale nel rendere il modello geocentrico non solo una teoria astratta, ma una realtà tangibile e comprensibile. Fornivano una mappa mentale dell'universo, un'immagine ordinata e gerarchica che si radicò profondamente nell'immaginario collettivo. La loro persistenza ben oltre l'inizio della rivoluzione scientifica testimonia la forza di questa visione del mondo e la lenta e complessa assimilazione del nuovo paradigma eliocentrico.

Riflessi Letterari: La Divina Commedia di Dante e Oltre

La letteratura, in particolare quella medievale, offre uno specchio fedele della pervasività del modello geocentrico, utilizzandolo non solo come sfondo descrittivo, ma come vera e propria impalcatura strutturale e simbolica per narrare viaggi ultraterreni, esplorare questioni morali e teologiche, e definire il posto dell'uomo nel creato.

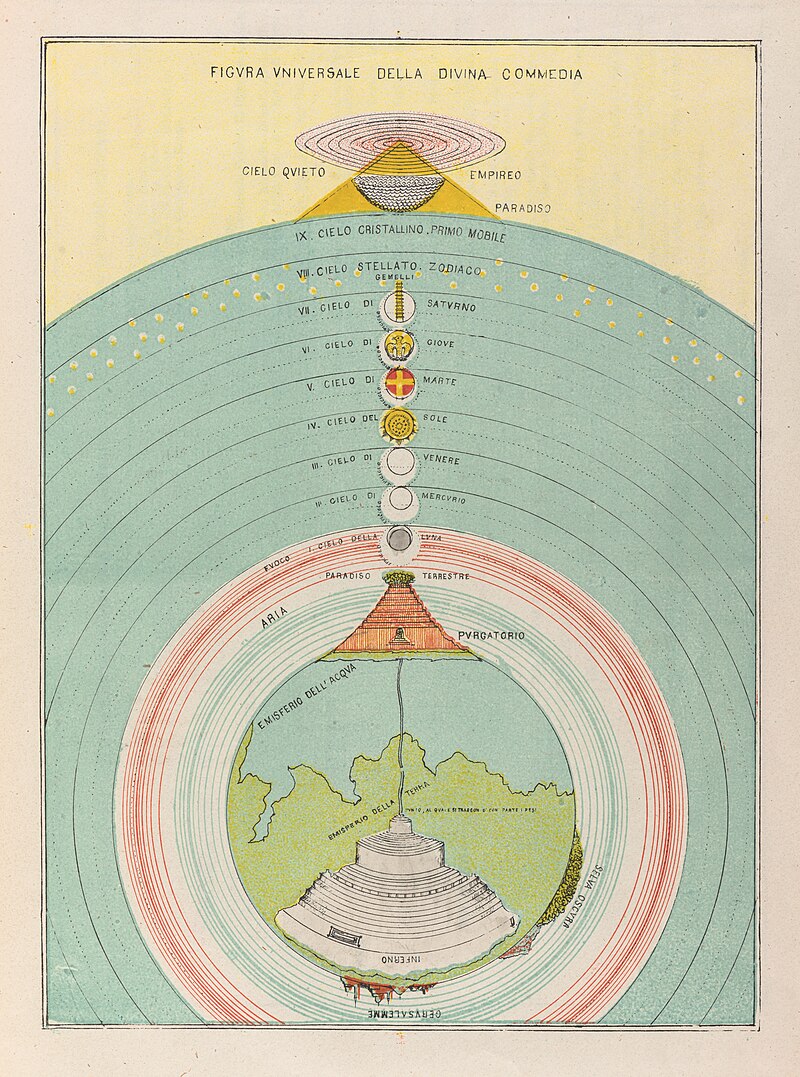L'esempio più grandioso e influente è senza dubbio la Divina Commedia di Dante Alighieri (inizi del XIV secolo), in particolare la terza cantica, il Paradiso. L'intera struttura del Paradiso dantesco è modellata sulla cosmologia geocentrica aristotelico-tolemaica, che Dante conosceva approfonditamente attraverso le fonti classiche e la filosofia scolastica. Il viaggio di Dante, guidato da Beatrice (simbolo della teologia e della grazia divina), è un'ascesa attraverso le nove sfere celesti concentriche che circondano la Terra immobile. Queste sfere, fatte di etere incorruttibile , sono, in ordine crescente di distanza dalla Terra: la Luna, Mercurio, Venere, il Sole, Marte, Giove, Saturno, la sfera delle Stelle Fisse (che contiene le costellazioni) e il Primo Mobile. Ogni sfera ruota attorno alla Terra, mossa dall'intelligenza angelica corrispondente e, in ultima analisi, dall'amore divino che emana da Dio. La velocità di rotazione aumenta progressivamente verso l'esterno. Al di là delle sfere fisiche e del tempo si trova l'Empireo, cielo immateriale, immobile e infinito, pura luce intellettuale e amore, che è la dimora propria di Dio, degli angeli e di tutte le anime beate.   

In questo grandioso edificio cosmico, Dante incontra diverse schiere di beati che gli si manifestano nelle varie sfere celesti, non perché quella sia la loro sede definitiva (che è l'Empireo), ma in base al grado della loro beatitudine e alla virtù che hanno esercitato in vita, in una perfetta corrispondenza tra ordine cosmico e ordine spirituale. Le prime tre sfere (Luna, Mercurio, Venere), che si trovano ancora parzialmente nell'ombra proiettata dalla Terra, ospitano le anime che mancarono in qualche misura nelle virtù cardinali (fortezza, giustizia, temperanza) a causa di influenze terrene (es. i voti infranti nella Luna). Le sfere successive ospitano esempi luminosi delle virtù: i sapienti nel Sole, i combattenti per la fede in Marte, i giusti governanti in Giove, gli spiriti contemplativi in Saturno. Nella sfera delle Stelle Fisse, Dante viene esaminato sulle tre virtù teologali (fede, speranza, carità). Il poema integra concetti chiave della fisica aristotelica, come la distinzione tra mondo sublunare corruttibile e cieli incorruttibili , e la dottrina del Primo Motore (identificato con Dio) come causa ultima del movimento universale. Anche la gravità è concepita aristotelicamente come la tendenza naturale dei corpi pesanti a dirigersi verso il centro della Terra, che coincide con il centro dell'universo.   

La Divina Commedia dimostra come il modello geocentrico fosse molto più di una semplice teoria astronomica: era una mappa completa del reale, fisico e metafisico, una struttura ordinata e significativa che permetteva di collocare l'esperienza umana, la storia della salvezza e la stessa natura di Dio all'interno di un quadro coerente e grandioso.

Ma Dante non fu l'unico. Molti altri autori medievali e tardo-antichi incorporarono la visione geocentrica nelle loro opere. Geoffrey Chaucer, contemporaneo di Dante, nei suoi Racconti di Canterbury e nel Troilus and Criseyde, fa riferimento alle influenze astrologiche dei pianeti (come Venere e Marte sulla Moglie di Bath ) e descrive l'ascesa dell'anima di Troilo attraverso le sfere celesti, da cui contempla "le stelle erranti" (i pianeti) e ascolta l'"armonia delle sfere", la musica prodotta dalla loro rotazione, un concetto di origine pitagorica popolare nel Medioevo. Anche Boezio, nel De Consolatione Philosophiae (VI sec.), evoca la struttura geocentrica con le sfere della Luna, del Sole e delle stelle. Persino nella letteratura latina classica, come nella Pharsalia di Lucano (I sec. d.C.), troviamo l'idea dell'anima che ascende attraverso le sfere dopo la morte. Il poeta epicureo Lucrezio, nel De rerum natura (I sec. a.C.), pur con una fisica diversa da quella aristotelica, difese anch'egli una visione geocentrica.   

Questi esempi mostrano come la cosmologia geocentrica fosse profondamente radicata nell'immaginario letterario per secoli. Essa forniva non solo un'ambientazione cosmica, ma anche un potente strumento simbolico per esplorare il destino umano, il rapporto con il divino e la struttura stessa della realtà. Il cosmo ordinato, finito e centrato sulla Terra era il palcoscenico naturale per il dramma umano e divino come concepito dalla cultura antica e medievale.

Integrazione Filosofica e Teologica (Scolastica, Tommaso d'Aquino)

L'autorità del modello geocentrico nel Medioevo fu enormemente rafforzata dalla sua integrazione nella filosofia Scolastica, il sistema di pensiero dominante nelle università europee tra il XII e il XVII secolo. La Scolastica si proponeva di conciliare la Rivelazione cristiana con la ragione filosofica, utilizzando principalmente gli strumenti concettuali e logici della filosofia di Aristotele, riscoperta in Occidente attraverso traduzioni dall'arabo e dal greco.  

L'opera di Aristotele, con la sua fisica, metafisica, logica ed etica, fornì alla Scolastica un sistema filosofico completo e coerente per comprendere il mondo naturale e il pensiero umano. Di conseguenza, anche la cosmologia aristotelica, con la sua Terra centrale e immobile e i suoi cieli perfetti e rotanti, fu ampiamente adottata e integrata nel quadro teologico cristiano.   

Tommaso d'Aquino (circa 1225-1274), la figura più eminente della Scolastica , svolse un ruolo cruciale in questa sintesi. Nella sua monumentale Summa Theologiae e in altre opere, Tommaso utilizzò la filosofia aristotelica come "ancella della teologia", impiegandone i concetti e le argomentazioni per chiarire e difendere le verità della fede cristiana. Egli accettò la struttura generale del cosmo aristotelico-tolemaico come la migliore descrizione scientifica disponibile del mondo fisico creato da Dio.   

Diversi aspetti della cosmologia aristotelica si prestavano particolarmente bene a un'interpretazione teologica:

Nonostante la sua resilienza e il suo profondo radicamento culturale, filosofico e teologico, il modello geocentrico portava in sé delle debolezze intrinseche e dovette affrontare sfide crescenti che, nel lungo periodo, ne minarono la credibilità e aprirono la strada all'affermazione del sistema eliocentrico. La crisi del geocentrismo non fu un evento improvviso, ma il risultato di una lenta erosione causata dalla convergenza di diversi fattori problematici.

• Complessità e mancanza di eleganza: come già notato, uno dei problemi più percepiti, anche se non necessariamente il più decisivo dal punto di vista scientifico, era la crescente complessità dell'apparato matematico richiesto per "salvare i fenomeni". La necessità di introdurre eccentrici, deferenti, epicicli e, soprattutto, equanti per ogni pianeta rendeva il sistema farraginoso e privo di quella semplicità ed armonia che molti filosofi e astronomi (fin da Platone) ritenevano dovesse caratterizzare la vera struttura del cosmo. La famosa (anche se apocrifa) battuta di Alfonso X  e la stessa motivazione iniziale di Copernico, che cercava un sistema più "razionale" e "armonico", riflettono questo disagio estetico e filosofico nei confronti di un modello percepito come eccessivamente artificioso.   
• Violazione dei principi fondamentali (Incoerenza Interna): la debolezza logica e filosofica più significativa risiedeva nell'uso dell'equante. Questo strumento, pur essendo cruciale per migliorare l'accuratezza predittiva del modello tolemaico, contraddiceva apertamente il principio metafisico del moto circolare uniforme attorno al centro geometrico dell'orbita, che era considerato un assioma fondamentale della fisica celeste aristotelica, la stessa fisica su cui si basava l'intero impianto geocentrico. Questa palese incoerenza interna tra i presupposti fisici del modello e gli strumenti matematici utilizzati per farlo funzionare fu uno dei principali motori delle critiche degli astronomi islamici e, successivamente, di Copernico stesso.   
• Problemi fisici e meccanicistici: al di là dell'incoerenza dell'equante, rimaneva problematico fornire una spiegazione fisica plausibile per l'intero meccanismo delle sfere, degli epicicli e dei deferenti. L'idea di sfere cristalline solide, ereditata da Aristotele, entrava in conflitto con la necessità, implicita nei modelli tolemaici, che le sfere o i meccanismi dei diversi pianeti potessero in qualche modo interpenetrarsi o interagire in modi complessi. Come potevano coesistere sfere materiali rigide con i moti epiciclici? Come si trasmetteva il moto da una sfera all'altra? Queste domande rimanevano largamente irrisolte, evidenziando una discrepanza tra la sofisticazione matematica del modello e la sua plausibilità fisica, come sottolineato già da Ibn al-Haytham.   
• Accuratezza predittiva limitata e necessità di aggiustamenti: Nonostante la sua complessità, il modello tolemaico non riuscì mai a raggiungere una precisione predittiva perfetta e duratura. Le discrepanze tra le previsioni e le osservazioni persistevano e tendevano ad accumularsi nel tempo, richiedendo continui aggiustamenti dei parametri o l'introduzione di ulteriori complicazioni. Questa incapacità di fornire previsioni definitive e stabili minava la fiducia nella sua validità ultima.   
• Mancanza di unità sistematica e connessioni arbitrarie: Il sistema tolemaico trattava il moto di ciascun pianeta (e del Sole e della Luna) in modo largamente indipendente, costruendo per ognuno un complesso meccanismo di cerchi su misura. Mancava una spiegazione unitaria e intrinseca che collegasse i moti dei diversi pianeti tra loro. Ad esempio, il fatto che i periodi degli epicicli dei pianeti superiori (Marte, Giove, Saturno) e i periodi dei deferenti dei pianeti inferiori (Mercurio, Venere) fossero tutti legati al periodo annuale del Sole appariva come una coincidenza inspiegabile all'interno del modello geocentrico. Anche la necessità di vincolare artificialmente i centri degli epicicli di Mercurio e Venere a rimanere sulla linea Terra-Sole sembrava un espediente ad hoc. Il modello copernicano, al contrario, avrebbe fornito una spiegazione naturale e unificante per queste correlazioni, legandole al moto orbitale della Terra stessa.   
• Incapacità di spiegare nuovi fenomeni osservativi: Infine, il colpo decisivo alla plausibilità fisica del modello geocentrico (sebbene non necessariamente alla sua utilità come strumento di calcolo) venne dalle scoperte rese possibili dall'introduzione del telescopio all'inizio del XVII secolo da parte di Galileo Galilei. Fenomeni come le fasi di Venere (che mostravano Venere illuminata dal Sole in modi spiegabili solo se orbitava attorno ad esso) e la scoperta delle lune di Giove (che dimostravano inequivocabilmente che non tutti i corpi celesti orbitavano attorno alla Terra) erano estremamente difficili da spiegare.

Tutto questo pose le basi per una nuova visione.