Le coordinate celesti: equatoriali

Abbiamo visto come osservare il cielo a occhio nudo possa sembrare semplice: basta individuare un astro e descrivere la sua posizione rispetto all’orizzonte e rispetto al Nord. Il sistema di coordinate altazimutali, che utilizza altezza e azimut per definire la posizione di un oggetto celeste, è intuitivo e quasi immediato, basta trovare la Polare per avere l'origine dell'azimut. Tuttavia, come accennato in apposita sede, presenta dei limiti fondamentali: le coordinate di ogni astro cambiano continuamente a causa della rotazione terrestre. Una stella che appare alta nel cielo a mezzanotte potrebbe essere sorta qualche ora prima e scomparire sotto l’orizzonte poco dopo. Questo rende il sistema altazimutale poco pratico per catalogare gli astri o per puntare con precisione un telescopio, tanto più che ogni osservatore, a seconda della sua posizione sulla Terra e del momento della notte, vedrà il cielo in modo diverso. Estrema variabilità nello spazio e nel tempo, quindi. 

Per superare questa difficoltà bisogna cambiare tipologia di osservatore e anziché costruire una sfera intorno a un singolo individuo (limitato peraltro dal fatto di trovarsi su un terreno e di avere, quindi, un orizzonte) la costruiamo intorno alla Terra intera: si immagini quindi una grande sfera ideale che circonda tutto il nostro pianeta e sul quale vengono proiettati gli altri astri, come se fossero fissati su uno schermo lontanissimo, dove i nostri occhi non riescono a cogliere le differenti distanze. Questo modello permette di considerare il cielo indipendentemente dal luogo e dal momento dell’osservazione, poiché è un cielo disegnato rispetto alla Terra intera e quindi lo stesso per ogni suo osservatore. Il sistema che ne deriva, di conseguenza, è un sistema di riferimento stabile e, relativamente a noi, universale.

Certo, a causa della rotazione terrestre ruota anche questa sfera celeste ma esistono punti su di essa che restano fissi e che quindi possiamo rintracciare sempre e utilizzare come riferimenti. Il primo passo è identificare il prolungamento dell’asse di rotazione terrestre, che individua i due poli celesti, e la proiezione del piano equatoriale, che diventa l’equatore celeste.

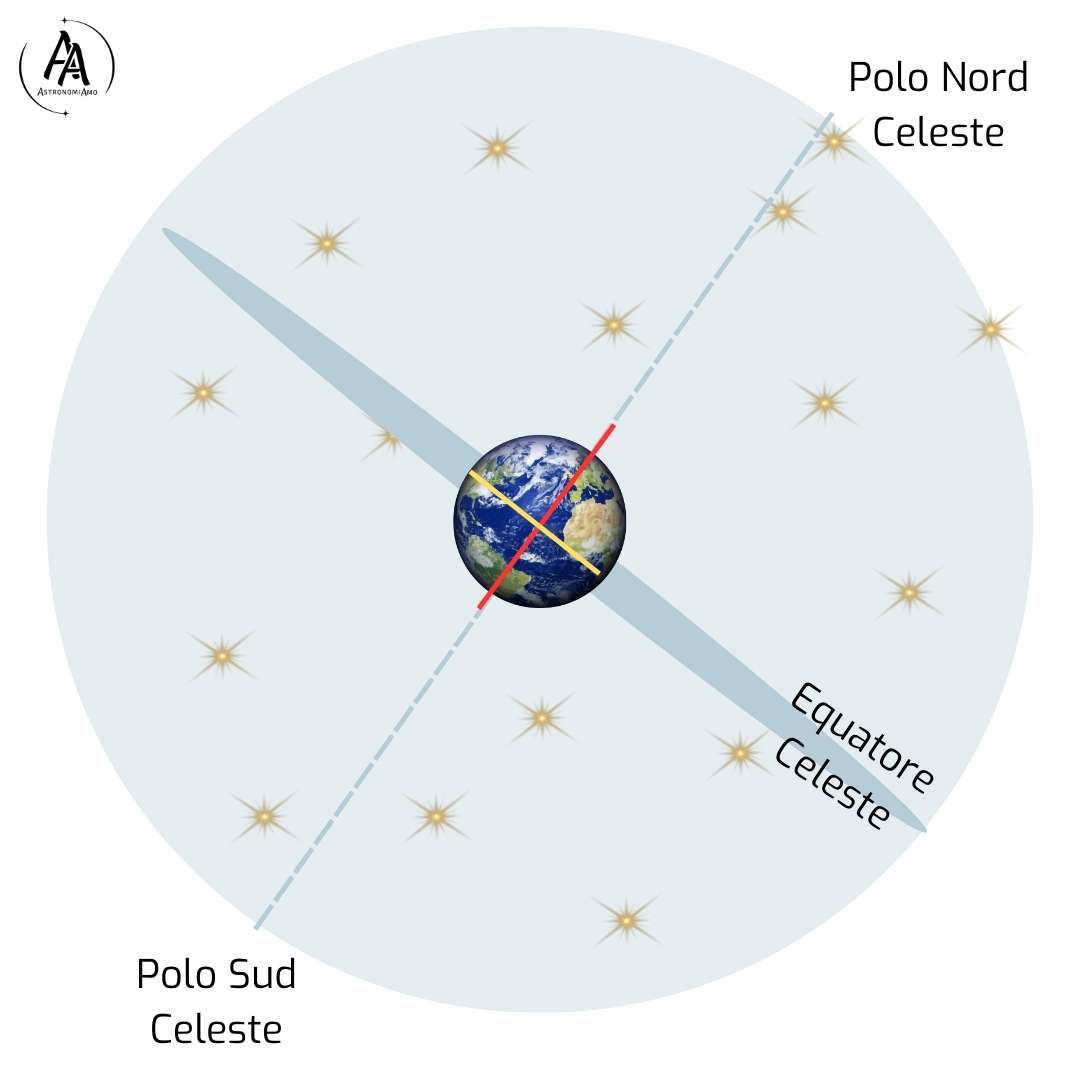Rappresentazione della sfera celeste. In evidenza i poli celesti e l'equatore celeste. I poli celesti sono il punto in cui la proiezione dell'asse del mondo (in rosso) "tocca" la sfera celeste, verso Nord e verso Sud. L'equatore celeste è la versione "allargata" dell'equatore terrestre (in giallo).

Come detto, ci sono punti che possiamo sempre calcolare abbastanza agevolmente conoscendo soltanto la latitudine del luogo in cui ci troviamo. Infatti, il Polo Nord Celeste si trova nel cielo a una altezza uguale a quella della latitudine dell'osservatore, mentre l'Equatore Celeste si trova sull'orizzonte opposto a una altezza pari a 90 - latitudine in valore assoluto.

Il sistema di coordinate celesti equatoriale è uno dei principali modi per localizzare le stelle e gli oggetti celesti nel cielo, equivalente al sistema di latitudine e longitudine usato sulla superficie terrestre ma proiettato sulla sfera celeste. È un sistema molto usato in astronomia perché è stabile nel medio periodo e non dipende dalla posizione del nostro punto di osservazione sulla Terra. In altre parole, le coordinate celesti equatoriali possono essere definite "fisse".

Il sistema di coordinate celesti equatoriale si basa su due elementi principali: l'ascensione retta (AR) e la declinazione (Dec). 

La declinazione

Si tratta, in pratica, dell'equivalente celeste della latitudine terrestre, indicando in parole semplici "quanti gradi un corpo celeste si trova sopra o sotto l'equatore celeste". Gli oggetti situati sull’equatore celeste hanno una declinazione di 0°, mentre quelli al polo nord celeste hanno una declinazione di +90° e quelli al polo sud celeste di -90°. Tra questi valori limite, come sempre, ci sono le condizioni intermedie. La declinazione, quindi, si misura in gradi, minuti e secondi. Valori positivi rappresentano corpi celesti dell'emisfero boreale mentre valori negativi fanno riferimento all'emisfero australe. 

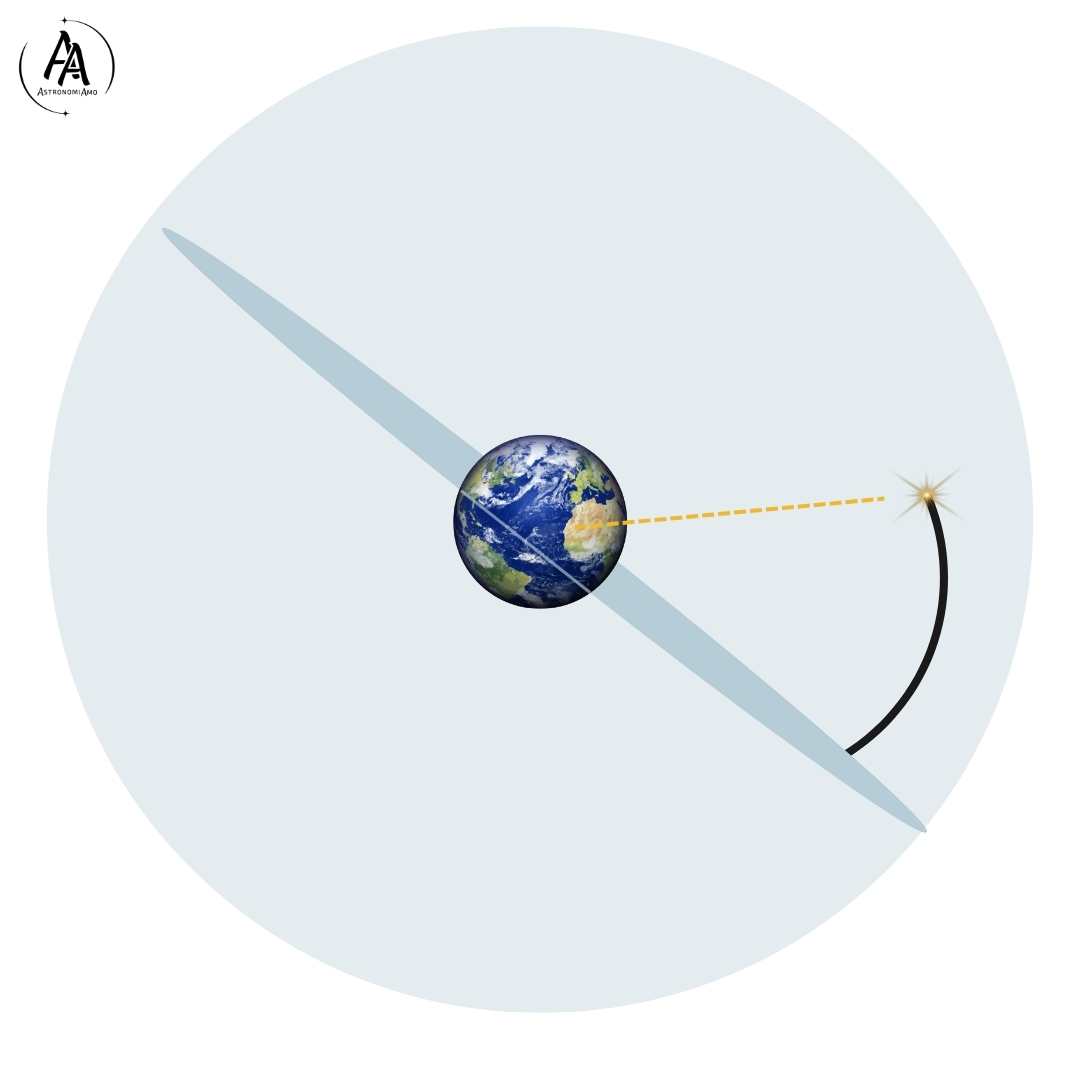Rappresentazione della declinazione: data una stella sulla sfera celeste, la declinazione è la distanza angolare della stella stessa rispetto all'equatore celeste.

L'Ascensione Retta

Prima di definire l'Ascensione Retta occorre fissarne l'origine. Per la declinazione il riferimento è l'equatore celeste quindi abbiamo una origine molto intuitiva, ma per l'Ascensione Retta bisogna spiegare qualcosa di più. Questo ruolo è svolto dal punto gamma, noto anche come punto vernale o punto d’Ariete. Il punto gamma è l’intersezione tra l’equatore celeste - che ben conosciamo - e il piano dell’eclittica, ovvero la traiettoria apparente che il Sole percorre nel cielo durante l’anno a causa del moto orbitale della Terra. In altre parole, è il movimento della Terra intorno al Sole ma visto da un osservatore terrestre tenendo di mira il Sole. 

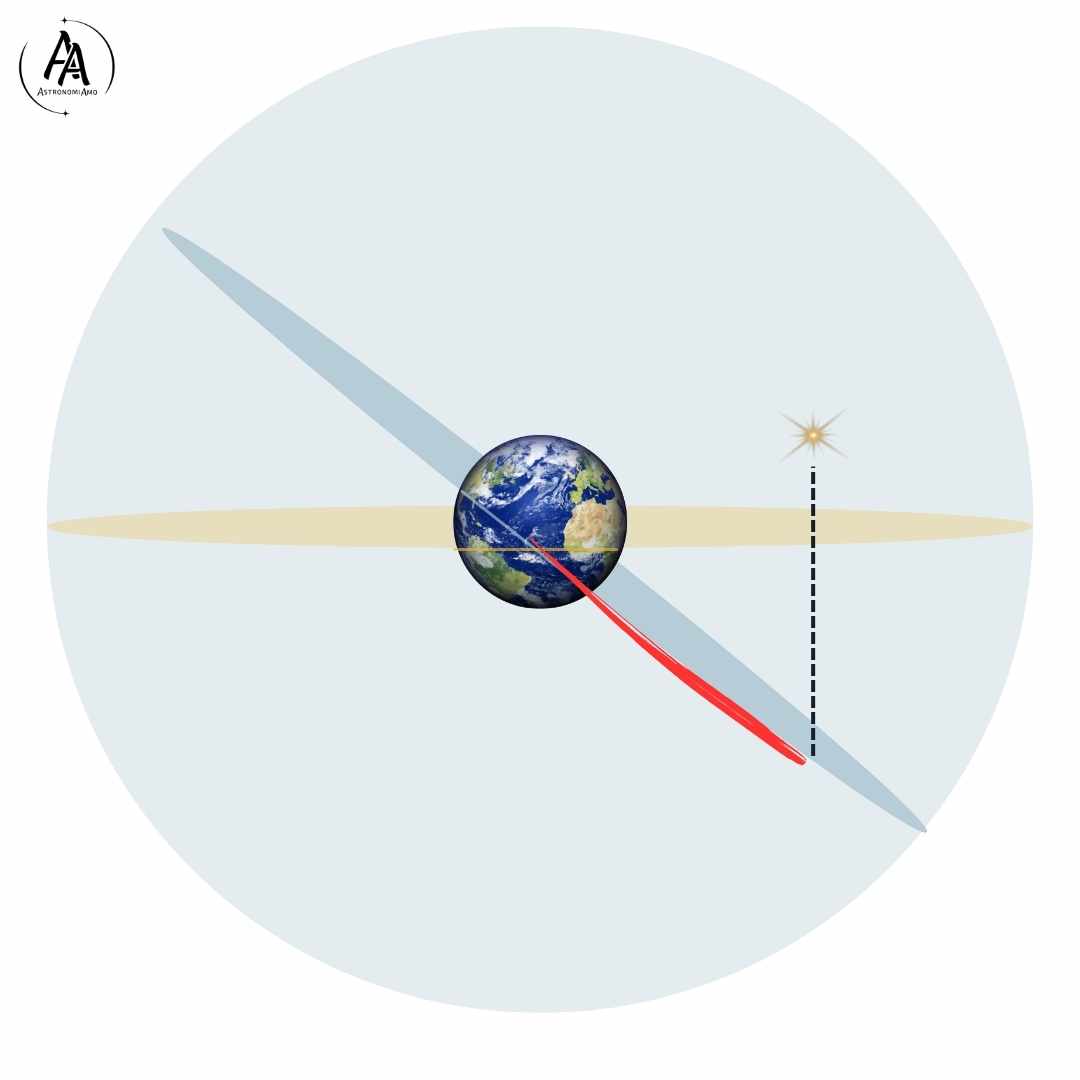Rappresentazione della ascensione retta: indicando con un piano rosa l'eclittica e un piano celeste l'equatore celeste, e quindi dato come punto vernale il punto della loro intersezione visibile nel centro della Terra, data una stella, l'ascensione retta è la distanza angolare tra questo punto e la proiezione della stella sull'equatore celeste (indicato da un arco rosso)

Il punto gamma viene quindi utilizzato come origine del sistema di coordinate equatoriali, in modo analogo a come il meridiano di Greenwich è il punto di riferimento per la longitudine terrestre. L’ascensione retta di un oggetto celeste si misura a partire da questa posizione, aumentando verso est lungo l’equatore celeste. Poiché la sfera celeste ruota apparentemente in circa 24 ore, l’ascensione retta è suddivisa in ore, minuti e secondi di tempo, dove 24 ore corrispondono a un angolo di 360°. Un'ora di Ascensione Retta corrisponde quindi a 15 gradi, il che vuol dire che un oggetto a 2 ore di ascensione retta si troverà a 30 gradi di distanza dal punto d'Ariete.

Ovunque ci troviamo, il cielo visibile dipende dalla posizione delle stelle rispetto all’orizzonte. Alcune di esse sono sempre presenti nel cielo, ruotando attorno alla Stella Polare senza mai tramontare. Queste sono chiamate "circumpolari" e comprendono quelle che si trovano abbastanza vicine al Polo Celeste. Altre stelle, invece, sorgono e tramontano nel corso della notte, risultando visibili solo in certi periodi dell’anno. Si trovano in una fascia intermedia del cielo, e la loro presenza dipende sia dalla stagione sia dall’ora della notte in cui si osserva. Infine, ci sono stelle che non compaiono mai sopra l’orizzonte. Queste si trovano troppo basse rispetto all'orizzonte dell'osservatore e rimangono sempre al di sotto della linea visibile del cielo, risultando completamente invisibili da questa latitudine. Data la latitudine del nostro luogo di osservazione, già dalla declinazione possiamo capire se un corpo celeste sarà o meno visibile durante il corso dell'anno (il periodo dipende anche dalla stagione, come vedremo)